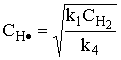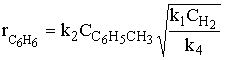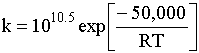Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 9: Reaction Mechanisms, Pathways, Bioreactions and Bioreactors

Chapter 9 Self Test

Pseudo Steady State Hypothesis

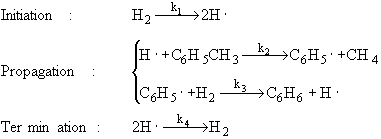
1)   An example of a gas phase chain reaction involving free radicals is hydrodealkylation, in which alkyl aromatics are converted to unsubstituted aromatics. A process for the hydrodealkylation of toluene from petroleum stocks to produce benzene and methane has been developed. The hydrodealkylation occurs in the gas phase at high temperature and involves free radical. The free radical mechanism is believed to proceed by the sequence

The specific reaction rates k1 and k4 are defined w.r.t. H2.

Derive the reaction rate law for the rate of formation of benzene based on this mechanism.

Hint: the reaction is 1/2 order in H2 and 1st order in toluene.


Solution

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution

 

For the elementary equation, we write the rate of formation of benzene as:

 

 

 (1)

We need to eliminate the concentration of the free radical by expressing it in terms of the concentrations of toluene and hydrogen.  Under psuedo-steady-state hypothesis, we set the rates of formation of and equal to zero, i.e.

 

 

 (2)

 

 (3)

Adding equations 2 and 3 yield

 

 

 (4)

Solving for   yields

 

 

 (5)

Solving for equation 3 for yields

 

 

 (6)

We can now eliminate from the reaction rate expression (1) to obtain

 

 

 (7)

 

(8)
where

 

(9)

 

Back to Chapter 9