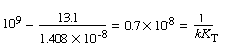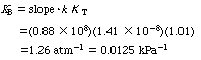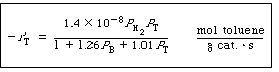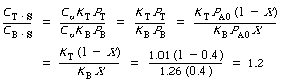Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 10: Catalysis and Catalytic Reactors

Learning Resources

Example CD10-2: Least Squares Analysis to Determine the Rate Law Parameters k, K T, and K B

(Example 6-2 in 2nd ed.)
       
       
   

Use the data in Table 10-6 together with Equation (10-81) to evaluate the rate law parameters. Then calculate the catalyst weight necessary for these rate law parameters.

  
       
   




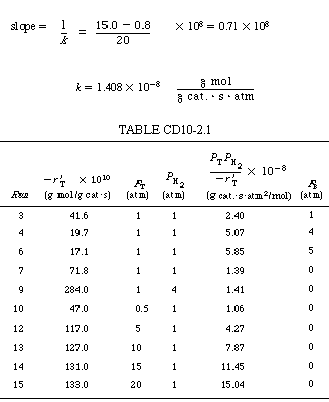
Solution

The calculations are shown in Table CD10-2.1. A plot ofimage 10eq133.gifversus P T at constant P B will be linear with slope 1/k (see Figure CD10-2.1).

  
       
   

image 10eq134.gif

 
       
   

Figure CD10-2.1

 
       
   

Rearranging Equation (10-81) for PB = 0, we have

  
       
   

image 10eq135.gif

(CD10-2.1)
       
   

From Figure CD10-2.1,

  
       
   

image 10eq136.gif

 
       
   

Substituting these values into Equation (CD10-2.1), we find that

  
       
   

image 10eq137.gif

(CD10-2.2)
     
   

The constant K B can be evaluated from the slope of the plot ofimage 10eq133.gifversus P B for constant P T . From Figure CD10-2.2,

  
       
   

image 10eq138.gif

 
       
   

Figure CD10-2.2

 
       
   

In addition to the graphical determination, we can use linear regression to determine the rate law parameters. We will use Equations (5-31) through (5-33) along with Table CD10-2.2 to determine k, K T , and
K B. in Equations (10-81) and (5-22).

Recall Equation (10-81),

  
       
   

image 10eq139.gif

(10-81)
       
   

and Equation (5-30),

  
       
   

image 10eq140.gif

(5-30)
       
   

where Y=image 10eq133a.gif, a 0 = 1/kK T, a 1 = K B /kK T , a 2 = 1/k, X 1 =P B , and X 2 = P T . Next, recall the linear regression equations and apply them for the 16 runs of this example.

  
       
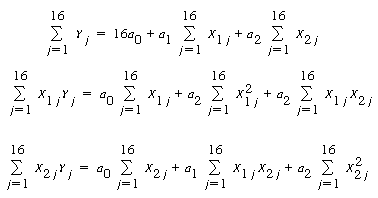
    image 10eq141.gif

(CD10-2.3)




(CD10-2.4)





(CD10-2.5)

   

If we were to use a software package such as POLYMATH, we would simply enter Y, X 1 X 2 , and for each run and the parameters a 0 , a 1 , and a 2 would be displayed in a few seconds. Alternatively, we can form Table CD10-2.2 and carry out the numerical operations ourselves to determine the rate law parameters. We can either form the table using a calculator or by using a spreadsheet such as Excel or Lotus 123.

  
       
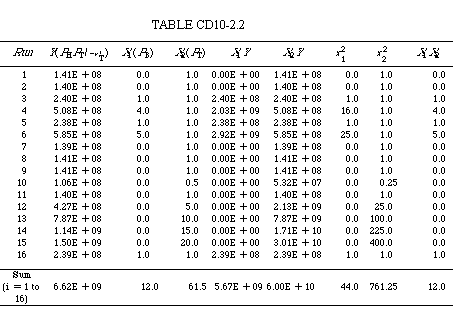
  image 10eq142.gif
       
   

Equation (CD10-2.3) becomes

  
       
   

6.62 X 109 = 16a0 + 12a1 + 61.5a2

(CD10-2.6)
       
   

Equation (CD10-2.4) becomes

  
       
   

5.67 X 109 = 12a0 = 44a = 12a21

(CD10-2.7)
   

Equation (CD10-2.5) becomes

  
       
   

6.0 X 1010 = 61.5a0 + 12a1 + 761.25a2

(CD10-2.8)
       
   

Solving these three equations simultaneously, we obtain a0 = 7.12 x 10 7 , a 1 = 9.0 x 10 7 , and a 2 = 7.16 x 10 7 . The corresponding rate law parameters are

  
  image 10eq146.gif  
       
   

Using POLYMATH, we obtain

  
       
   

image 10eq147.gif

 
       
   

with, of course, the parameter values being the same as those obtained from Table CD10-2.2 and Equation (CD10-2.5).

After substituting the numerical values of k, KB , and K T into Equation (10-80), the rate law at 600°C for hydrodemethylation of toluene,

image 10eq148.gif

is given by the equation

 
       
   

image 10eq149.gif

(CD10-2.9)
       
   

whereP i is in atm.

  
       
   

After we have the adsorption constant K T and K B , we could calculate the ratio of sites. For example, the ratio of toluene sites to benzene sites at 40% conversion is

image 10eq150.gif
   

We see that at 40% conversion there are approximately 20% more sites occupied by toluene than by benzene.

  
       
       
       
   

Calculate the catalyst weight necessary for these parameters:

  
   

If we were to neglect pressure drop, we can solve for the catalyst weight necessary to achieve 65% conversion with the aid of Simpson's five-point formula.

  
       
   

image 10eq151.gif

 
       
   

Substituting for k, K T , K B ,P B , PH 2, and PT in Equation (E10-3.2) yields

  
       
   

10eq152.gifimage

(CD10-2.10)
       
   

We can now proceed to solve for the catalyst weight necessary to obtain this conversion by using Equation (CD10-2.10).

  
       
   

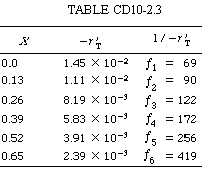
Hand calculations: The calculations for X versus (1/) are displayed in Table CD10-2.3.

  
       
   

image 10eq153.gif

 
       
   

Using numerical integration (Appendix A.5), after dividing the area under the curve into two parts: X = 0 to X = 0.52 with h 1 = 0.13 and X = 0.52 to X = 0.65 with h 2 = 0.13, we have

  
       

Numerical
evaluation

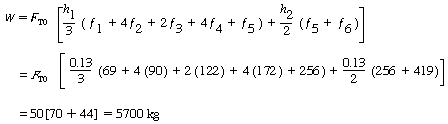   image 10eq154.gif
       
   

Since the reciprocal of the rate of reaction increases sharply as the conversion approaches unity, the numerical integration probably should have included a greater number of integrals than the six used in the calculation.