| Select Chapter >> | TOC | Preface | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Appendices |
Chapter 10: Catalysis and Catalytic Reactors
Professional Reference Shelf
The following information is taken from the 4th edition of Elements of Chemical Reaction Engineering, so the equation numbers correspond to those found in that bookR10.2 Hydrogen Adsorption
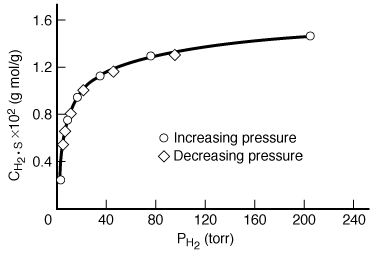
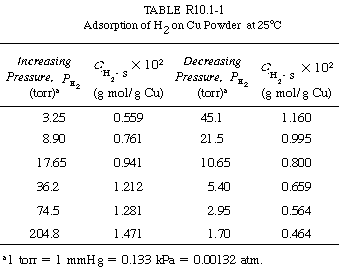
| Consider the adsorption of a non-reacting gas onto the surface of a catalyst. Adsorption data are frequently reported in the form of adsorption isotherms. Isotherms portray the amount of a gas adsorbed on a solid at different pressures but at one temperature. A typical adsorption isotherm, shown in Figure R10.1-1, is taken from the classic study of Ward, 1 who adsorbed hydrogen on powdered copper at 25°C (see Table R10.1-1). The data appear to be quite precise. Only one point is slightly off a smooth curve, and there is no hysteresis because the points taken while the pressure was being gradually increased lie on the same curve as those taken while the pressure was decreased. |
||
Figure R10.1-1 |
||
|
||
|
Postulate models, then see which one(s) fit(s) the data |
This isotherm can be used to gain insight into the adsorption process. An equation for the curve in Figure R10.1-1 will be derived, and the derivation will reveal significant properties of the hydrogen-copper system. First, a model system is proposed and then the isotherm obtained from the model is compared with the experimental data shown on the curve. If the curve predicted by the model agrees with the experimental curve, the model may reasonably describe what is occurring physically in the real system. If the predicted curve does not agree with that obtained experimentally, the model fails to match the physical situation in at least one important characteristic, and perhaps more. To describe Ward's data, two models will be postulated--one in which hydrogen is adsorbed as molecules, H 2 , on copper powder, and the other in which hydrogen is adsorbed as atoms, H, instead of molecules. |
|
|
Two models: |
The former is called molecular or nondissociated (e.g., H 2 ) adsorption and the latter is called dissociative adsorption. Whether a molecule adsorbs nondissociatively or dissociatively depends on the metal (M) surface. For example, CO undergoes dissociative adsorption on iron and molecular adsorption on nickel. |
|
|
||
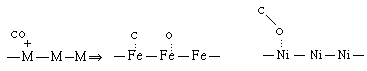
A. Molecular Adsorption
|
||
|
(R10.1-1) |
|
|
In obtaining a rate law for the rate of adsorption, the reaction in
Equation (R10.1-1) can be treated as an elementary reaction. The rate of
attachment of the hydrogen molecules to the surface is proportional to the number of
collisions that these molecules make with the surface per second. In other words, a
specific fraction of the molecules that strike the surface become adsorbed. The
collision rate is, in turn, directly proportional to the hydrogen partial pressure,
|
|
rate of attachment |
||
The rate of detachment of molecules from the surface can be a
first-order process; that is, the detachment of hydrogen molecules from the surface
is usually directly proportional to the concentration of sites occupied by the
molecules, |
||
| rate of detachment |
||
| The net rate of adsorption is equal to the rate of molecular attachment to the surface minus the rate of detachment from the surface. If k A and k -A are the constants of proportionality for the attachment and detachment processes, then |
||
|
(R10.1-2) |
|
|
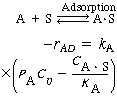
( The ratio K A = k A / k - A is the adsorption equilibrium constant. Using it to rearrange Equation (R10.1-2) gives |
|
|
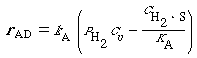
(R10.1-3) |
|
|
The parameters k A , k -A , and K A are all functions of temperature, exhibiting an exponential temperature dependence. The forward and reverse specific reaction rates, k A and k -A increase with increasing temperature, while the adsorption equilibrium constant, K A , decreases with increasing temperature. At a single temperature, in this case 25°C, they are, of course, constant in the absence of any catalyst deactivation. |
|
Because hydrogen is the only material adsorbed on the catalyst, the site balance gives |
||
|
(R10.1-4) |
|
|
The points plotted in Figure R10.1-1 were taken at equilibrium conditions. The experimental details present in the original work support this fact, and the absence of hysteresis confirms it. At equilibrium, the net rate of adsorption equals zero. Setting the right-hand side of Equation (R10.1-3) equal to zero and solving for the concentration of H 2 adsorbed on the surface, we get |
|
|
(R10.1-5) |
|
Using Equation (R10.1-4) to give C |
||
|
||
| Rearranging gives us |
||
|
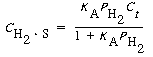
(R10.1-6) |
|
|
Langmuir isotherm for adsorption of molecular hydrogen |
This equation thus gives |
|
|
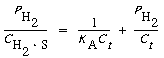
(R10.1-7) |
|
and the linearity of a plot of |
||
B. Dissociative Adsorption
|
||
|
||
| When the hydrogen molecule dissociates upon adsorption, it is referred
to as the dissociative adsorption of hydrogen. As in the case of molecular
adsorption, the rate of adsorption here is proportional to the pressure of hydrogen
in the system, because this rate governs the number of gaseous collisions with the
surface. For a molecule to dissociate as it adsorbs, however, two adjacent vacant
active sites are required rather than the single site needed when a substance adsorbs
in its molecular form. The probability of two vacant sites occurring adjacent to one
another is proportional to the square of the concentration of vacant sites. These two
observations mean that the rate of adsorption is proportional to the product of the
hydrogen partial pressure and the square of the vacant site concentration, |
||
| For desorption to occur, two occupied sites must be adjacent, meaning
that the rate of desorption is proportional to the square of the occupied-site
concentration,
( |
||
|
(R10.10-8) |
|
|
On this particular |
Figure R10.1-2 |
|
|
||
|
Rate of |
|
|
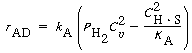
| where |
||
|
||
At equilibrium, r AD = 0, and |
||
|
||
| or |
||
|
(R10.1-9) |
|
| From Equation (R10.1-1), |
||
|
||
| This value may be substituted into Equation (R10.1-9) to give an
expression that can be solved for |
||
|
Langmuir isotherm for adsorption as atomic hydrogen |
|
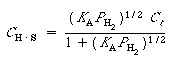
(R10.1-10) |
Taking the inverse of both sides of the equation, and then multiplying
through by |
||
|
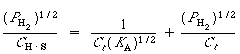
(R10.1-11) |
|
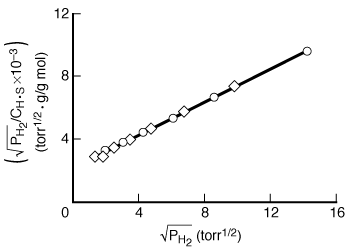
This equation is the linearized Langmuir isotherm for dissociative
adsorption. It says that if the hydrogen is dissociatively adsorbed on the copper,
a straight line should result when |
||
|
The dissociative |
The data in Figure R10.1-1 are replotted in Figure R10.1-3 in the form suggested by Equation (R10.1-11). An excellent straight line is obtained, giving support to the postulate of hydrogen being dissociatively adsorbed on the copper powder. A comparison of the results of the models indicates that hydrogen is adsorbed on the copper as atoms rather than as molecules. Hydrogen-deuterium tracer studies have confirmed this interpretation. Some comments seem deserved here. The data presented seemed very precise. If they had not been so, and there had been significant scatter, it would have been impossible to distinguish between the two models. The curvature in Figure R10.1-2 is slight, so the difference between the two plots is somewhat subtle. A discerning eye is necessary to distinguish between the two mechanisms in this situation. This subtle difference is one reason why this type of agreement between a model and the behavior of experimental data usually requires supporting spectroscopic and tracer experiments.
Figure R10.1-3 |
.
Because hydrogen molecules can adsorb only on vacant sites and not on sites already
occupied by other hydrogen molecules, the rate of attachment is also directly
proportional to the concentration of vacant sites,
C
. Combining these two facts means
that the rate of attachment of hydrogen molecules to the surface is directly proportional to the product of the partial pressure of H and
the concentration of vacant sites:
as a function of
.
, yields
is plotted as a function of
.