Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 12: Steady-State Nonisothermal Reactor Design: Flow Reactors with Heat Exchange

R12.2 Steady-State Bifurcation Analysis

All equation numbers refer to 4th edition of Elements of CRE

    In reactor dynamics it is particularly important to find out if multiple stationary points exist or if sustained oscillations can arise. Bifurcation analysis is aimed at locating the set of parameter values for which multiple steady states will occur.1 We apply bifurcation analysis to learn whether or not multiple steady states are possible. A bifurcation point is a point at which two branches of a curve coalesce as a parameter is varied. Consider the function image 08eq34.gif, in which x is a scalar variable and lambda gif is a parameter. Figure DVD12-1 shows curves (AB, BC, and BD) for which  
       
    (DVD12-1)
       
    is satisfied. We see that as we start to increase TIME GIF along AB, there is only one value of x for a given lambda gif that will satisfy Equation (DVD12-1). However, as we continue to increase along AB, we reach a bifurcation point * beyond which there are two values of x that satisfy Equation (DVD12-1) for a given value of lambda gif. Consequently, we analyze our system of equations to learn if a bifurcation point exists that denotes multiple solutions.

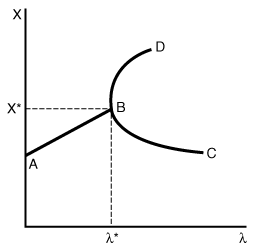There is another condition that is necessary for a bifurcation point to exist. If we were to move an incremental amount delta lambda gif away from the bifurcation point but still remain on BC or BD, we would have		  
       
    IMAGE 08eq37.gif (DVD12-2)
       
   

Figure DVD12-1
Bifurcation point.

 
       
    Expanding Equation (DVD12-2) in a Taylor series, it can be shown that at the bifurcation point  
       
    image 08eq38.gif (DVD12-3)
       
    If Equations (DVD12-1) and (DVD12-3) are satisfied, there will be a set of parameter values for which we will have multiple steady states (MSS).

We shall continue the discussion of the first-order reaction taking place in a CSTR to illustrate bifurcation analysis. A slight rearrangement of a combination of Equations (8-68) and (8-69) from the energy balance gives		  
       
    image 08eq39.gif (DVD12-4)
       
    which is of the form  
       
    image 08eq40.gif (DVD12-5)
       
    where greeka.gif and beta gif are positive constants.  
       
    Similarly, with some minor manipulation, the mole balance on an isothermal CSTR can be put in similar forms,  
       
    image 08eq41.gif (DVD12-6)
       
    or  
       
    image 08eq42.gif
(DVD12-7)
    We observe that both the CSTR energy and mole balances are of the form  
       

  IMAGE 08eq43.gif (DVD12-8)
    If F(y) is a monotonically increasing function as shown in Figure DVD12-2, the derivative of the function with respect to y will never be zero, that is,  
       
    IMAGE 08eq44.gif  
       
    Upon differentiating Equation (DVD12-8), we have (DVD12-9)
    IMAGE 08eq45.gif  
       
    and we see that dF/dy can never be zero if the maximum value of the derivative of G is less than greeka. Thus the sufficient condition for uniqueness is  
       
Uniqueness
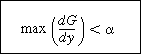
   IMAGE 08eq46.gif (DVD12-10)
       
    When Equation (DVD12-10) is satisfied there will be no multiple steady states. However, if max 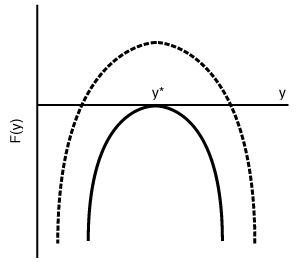IMAGE 08eq47.gif, we do not know at this point whether or not multiple solutions exist and we must carry the analysis further.

Figure DVD12-2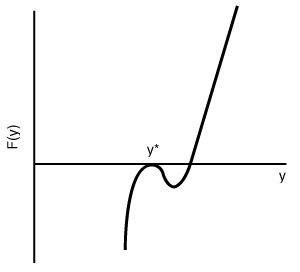
MSS with a parabolic function.




Figure DVD12-3
F(y ) curve common to chemically reacting systems.

We now apply the condition for a bifurcation point, Equations (DVD12-1) and (DVD12-3), to the CSTR balances, that is, Equation (DVD12-8). If multiple steady states exist, there will be a bifurcation point, y*, at which the following conditions are satisfied:

 
       
Conditions for
multiple steady states
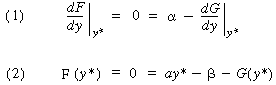
   IMAGE 08eq48.gif (DVD12-11)

(DVD12-12)
       
       
    Figure DVD12-2 shows that a parabola satisfies both conditions (1) and (2), that is, Equations (DVD12-11) and (DVD12-12), respectively. Consequently, we see that there will be a set of parameter values for which multiple solutions will exist, as demonstrated by the dashed-line parabola. Figure DVD12-3 shows the shape of a typical curve in reaction systems with multiple steady states.