| Select Chapter >> | TOC | Preface | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Appendices |
Chapter 12: Steady-State Nonisothermal Reactor Design: Flow Reactors with Heat Exchange
Multiple Reactions in a PFR with Variable Coolant Temperature
The irreversible liquid phase reactions
Reaction (1)
Reaction (2)
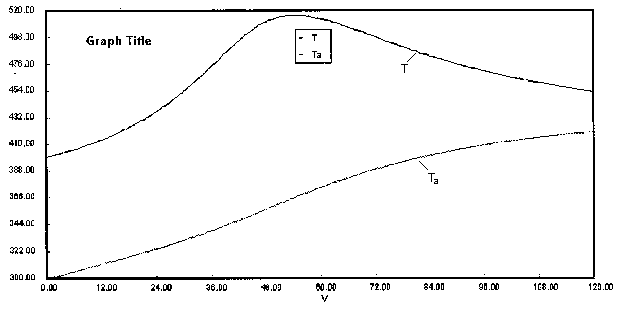
are carried out in a PFR with heat exchange. The following temperature profiles were obtained for the reaction mixture and the coolant stream.
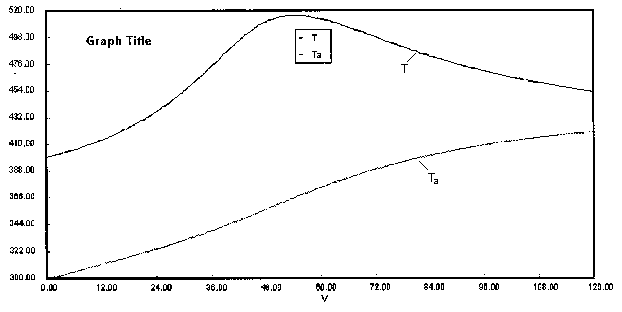
The concentrations of A, B, C, and D were measured at the point down the reactor where the liquid temperature, T, reached a maximum of 516K at 54 dm3. The concentrations at the maximum temperature were found to be CA = 0.05, CB = 0.22, CC = 0.245, and CD = 0.055 all in mol/dm3. The product of the overall heat transfer coefficient and the heat exchanger area per unit volume, Ua, is 5 cal/s•m3•K. The mole feed rate of A is 2 mol/s and the entering molar flow rate of B is 4 mol/s. The volumetric feed rate is 10 dm3/s which the molar flow rate of inerts is 0.5 mol/s. What is the activation energy for Reaction (1)? E1 =
Additional Information
Coolant flow rate = 25 g/s, and Coolant heat capacity = 20 cal/g•K
Hint 1: What is the energy balance?
Hint 2: What is Qr?
Hint 3: What are Qg1 and Qg2?
Hint 1. What is the energy balance?
The energy balance is
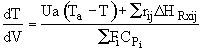
For the two reactions given here the heat of reaction for reaction (1) is in terms of A and for reaction (2) it is in terms of B
At the maximum the derivative of T wrt V is zero.
then
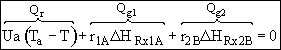
Hint 2. What is Qr?
Qr
Hint 3. What are Qg1 and Qg2?
Note a quick check shows DCp = 0 for both reactions
Reaction 1
Reaction 2
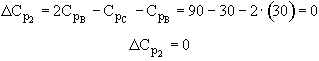
Therefore both heats of reaction are independent of temperature!!
Qg1 = r1A DHRx1A
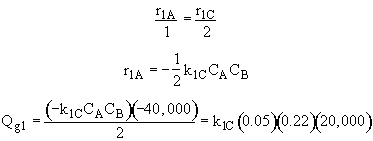
Qg2 = r2B DHRx2B
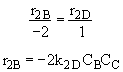
From the temperature dependence given in the problem statement
we note at 516 K that 
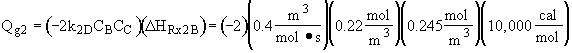
Full Solution
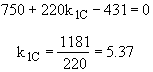
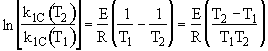
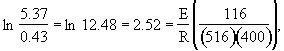
