Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 13: Unsteady State Nonisothermal Reactor Design

Example DVD13-3: Falling Off The Steady State

 

Propylene glycol is produced in a CSTR in which precautions have been taken to prevent product loss. Propylene oxide (A) is fed to a 413-gal reactor at a rate of 300 lb mol/h at a temperature of 75°F. Water (B) is fed at a rate of 2000 lb mol/h and methanol at a rate of 20 lb mol/h. Determine what happens to a CSTR operating at 172°F and a conversion of 86.4% when there is a drop in feed temperature from 75°F to 68°F.

  
     
 
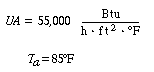image 09eq39.gif
  
     
 

 

  
     
 




Solution

  
     
 

We will first look at the steady-state conditions before the upset occurred. The mole balance conversion is:

  
     
 
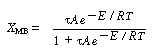image 09eq40.gif

 
     
 

The energy balance conversion is:

  
     
 
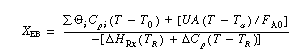image 09eq41.gif

 
     
 

Neglectingimage 09eq42.gifand substituting the appropriate values, we have

  
     
 
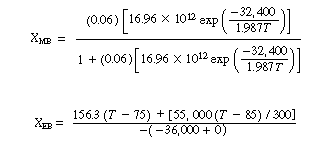image 09eq43.gif

(CDE13-3.1)




(CDE13-3.2)
     
 

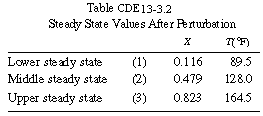
If we were to plot XEB and XB as a function of temperature, we would we see that there are three steady-state conditions for this set of parameter values (Table CDE13-3.1). Before the drop in feed temperature occurred we operated at the upper steady state (T = 172°F, X = 0.864). The ignition temperature of the feed is 78°F, and the extinction temperature is 61°F .

  
     
 
imag e09eq44.gif
 
     
 

We will now consider what happens when an upset occurs while operating at the upper steady state. Say that the inlet temperature drops from 75°F to 68°F. Figure CDE13-3.1 shows the corresponding XEB and XMB curves after this drop. There are still three steady states (Table CDE13-3.2) for this new inlet temperature, indicating that we have not dropped below the extinction temperature of 61°F.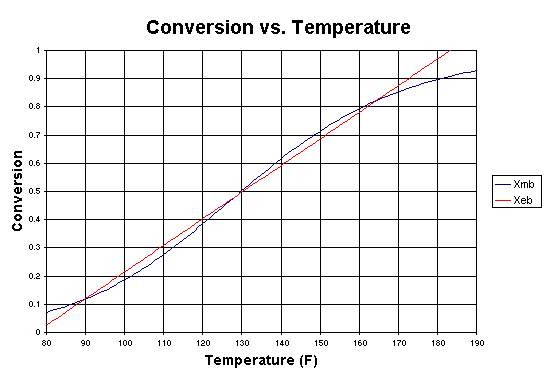



Figure CDE13-3.1
XEB and XMB after TO perturbation.

 
  
     
 

image 09eq45.gif

 
  
     
 

Based on a steady-state analysis, it would appear that after the drop in the inlet temperature we should remain at the upper steady state with T = 164.5°F and X = 82.3%. However, using a dynamic simulation (see the development in the equations below) with POLYMATH (Table CDE13-3.3), we will see that with this perturbation in the inlet temperature, the conversion and temperature drop to the lower steady-state values, as shown in Figure CDE13-3.2.


TABLE CDE13-3.3




Figure CDE13-3.2
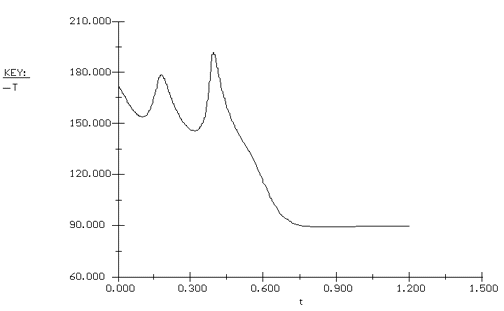
Temperature Time Trajectory



 
     
 



Unsteady-State Equations After Temperature Perturbation
Although there are slight differences in the densities of the liquid species, we shall assume constant density.

  
     
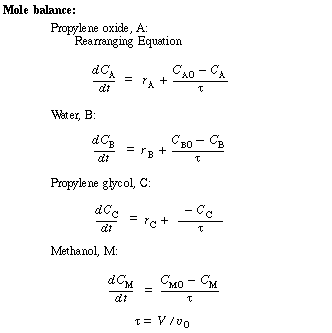
  image 09eq46.gif  
   
     
 

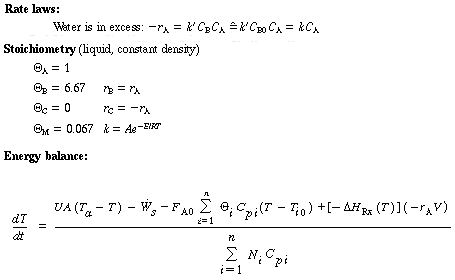
For constant volume, constant heat of reaction, and no work done by the system, when applied to this example becomes

  
     
 
image 09eq48.gif
  
     
 

The number of moles Ni in the denominator is just Ni = CiV.

  
     
 
image 09eq49.gif

 
     
 

We see that even though the entering temperature did not drop below the extinction temperature, the perturbation in the entering temperature was large enough to drive the temperature and conversion drop to their lower steady-state values of 89.5°F and 11.6%, respectively. To prevent this problem of moving to an undesired steady state, a control system is usually incorporated into the reactor system.