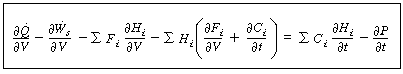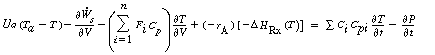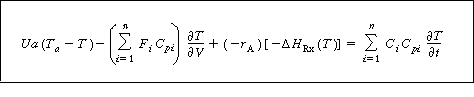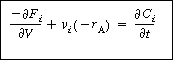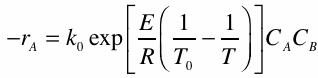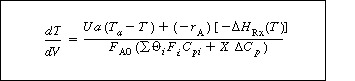Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 13: Unsteady State Nonisothermal Reactor Design

Professional Reference Shelf

R13.7 Unsteady Operation of Plug-Flow Reactors

   

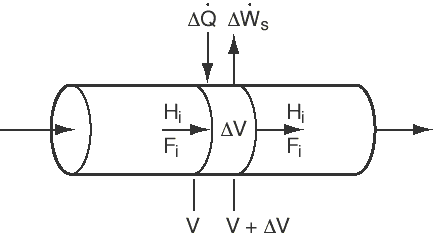
We plan to reduce the energy balance into a more usable form. To achieve this form for plug-flow reactors, we begin by applying the balance to a small differential volume,image 09eq51.gif, in which there are no spatial variations (Figure R13.7-1). The number of moles of species i inimage 09eq51.gifis

  
       
   

image 09eq52.gif

 
       
       
   

Figure CD13.7
PFR with heat gain or loss.

  
       
       
   

Substituting for Ni and dividingimage 09eq51.gifby gives

  
       
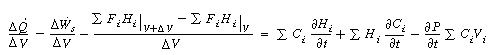
    image 09eq53.gif
       
   

Taking the limit asand noting that gives

  
       
   

image 09eq56.gif

 
       
   

Rearranging, we have

  
       
   

image 09eq57.gif

(R13.7-1)

       
   

Comparing Equations (R13.7-1) and (R13.7-2)

  
       
   

image 09eq58.gif

(R13.7-2)
       
   

we note that the term in parentheses is just ri. The rate of reaction of species i is related to the rate of disappearance of species A through the stoichiometric coefficient, 

  
       
   

image 09eq59.gif

 
       
   

Then

  
       
   

image 09eq60.gif
       
   

Finally,

  
       

 

  

image 09eq61.gif

  
       
   

where a is the heat exchange area per unit volume. Differentiating yields

  
       
   

image 09eq62.gif

 
       
   

Recalling that

  
   

image 09eq63.gif

 
       
   

we substitute these equations to obtain

  
       
   

image 09eq64.gif
       
   

Neglecting shaft work and changes in pressure with respect to time, we obtain

  
       

Transient energy
balance on a PFR

  

image 09eq65.gif

(R13.7-3)
   

This equation must be coupled with the mole balances,

  
     

(R13.7-4)

Numerical solution
required for these
three coupled equations

  

image 09eq66.gif

 
       
   

and the rate law,

  
       
   

image 09eq50.gif

(R13.7-5)
       
   

and solved numerically. A variety of numerical techniques for solving equations of this type can be found in the book Applied Numerical Methods.1

We note, however, one can approximate the partial differential equation (PDE) of the unsteady PFR energy balance by replacing the PFR with a number of CSTRs in series. One then simply solves the coupled ODEs using Polymath™ or MATLAB™.

For steady-state operation in which no work is done by the system, Equation (R13.7-3) reduces to

  
       
   

image 09eq68.gif

(R13.7-6)
       
   

Substitution for the molar flow rates Fi in terms of conversion gives Equation (R13.7-7).

  
       

Use this
equation for
steady-state
energy balance on a PFR
with heat transfer

  

image 09eq69.gif

(R13.7-7)
       
   

As stated previously, this equation is solved simultaneously with the mole balance.