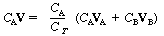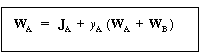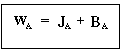Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Learning Resources

Example CD14-2: Relating the Fluxes WA, BA, and JA

    Derive Equation (11-6) starting from the fact that the molecular diffusional flux is the flux relative to the molar average velocity.  
       
   

Solution

  
    The difference in velocities (VA -V) tells us the velocity at which species A is moving relative to the average velocity of all the species. The diffusive flux JA of A relative to the molar average velocity is  
       

Velocity of A
relative to the average
velocity of all
the species

 

JA = CA (VA -V)


JA = CAV A -CAV

(CDE11-2.1)

(CDE11-2.2)

    Using Equation (11-3) yield  
       
   

JA = WA -CAV

(CDE11-2.3)
       
    Rearranging gives us  
       
   

WA = JA +CAV

(CDE11-2.4)
       
    The second term on the right-hand side can be expanded to  
       
   

CAV = CA(yAVA + yBVB)

(CDE11-2.5)
       
    Factoring the reciprocal of the total concentration, 1/CT, from the term in parentheses, we have  
       
   



= yA(WA + WB)

(CDE11-2.6)
    Then  
       
   

image 11eq17.gif

(11-6)
   
 
Recalling that

BA = CAV

   = YA (WA + WB