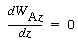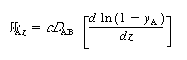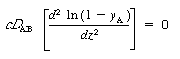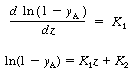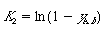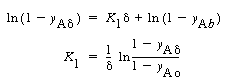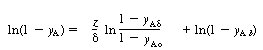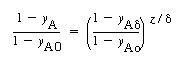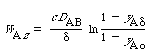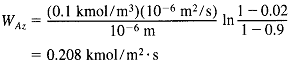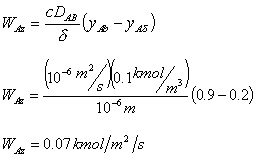Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 14: External Diffusion Effects on Heteregeneous Reactions

Learning Resources

Example CD14-3: Diffusion Through a Stagnant Gas

    Calculate the steady-state concentration profile and diffusion rate for the diffusion of gas A through a stagnant gas B. The geometry (Figure E11-2.1) and boundary conditions are identical to those given in Example 11-2. The pressure and temperature, and hence the total concentration, are constant throughout the system.

Solution

Steps 1 and 2:
The procedure for obtaining the differential of the molar flux with respect to distance is identical with that for the diffusion of species A through a liquid. Consequently, we can start with Equation (E11-1.3):		  
       

Mole balance

 

image 11eq18.gif

(E11-1.3)
       
    Step 3: We now need to relate the flux to concentration. Recalling the discussion in Section 11.2.1 and Equation (11-19), for diffusion through a stagnant film we have  
       

Evaluating bulk
flow term

 

image 11eq19.gif

(CDE11-3.1)
       
    Combining Equations (CDE11-1.1) and (E11-1.3) yields  
       
   

image 11eq20.gif

 
       
    or  
       

Differential
equation

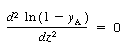image 11eq21.gif

(CDE11-3.2)

 
       
    Integrating, we obtain  
       
   

image 11eq22.gif

(CDE11-3.3)


(CDE11-3.4)
       
    Step 4: The constants of integration can be evaluated using the following boundary conditions:  
       







Boundary conditions

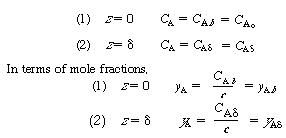
  image 11eq23.gif






(CDE11-3.5)


(CDE11-3.6)
       
    Step 5: Applying the first boundary condition, we obtain  
       
   

image 11eq24.gif

(CDE11-3.7)
       
    Using the second boundary condition yields  
       
   

image 11eq25.gif





(CDE11-3.8)
       
    Combining Equations (CDE11-3.4), (CDE11-3.7), and (CDE11-3.8) gives us  
       
   

image 11eq26.gif

(CDE11-3.9)
       
    Rearranging yields  
       

Concentration
profile

 

imag e11eq27.gif

(CDE11-3.10)
       
    The concentration profile is shown in Figure CDE11-3.1. The concentration profiles for the case of dilute gas or EMCD are compared with diffusion through a stagnant film in Figure CDE11-3.1.


  
 

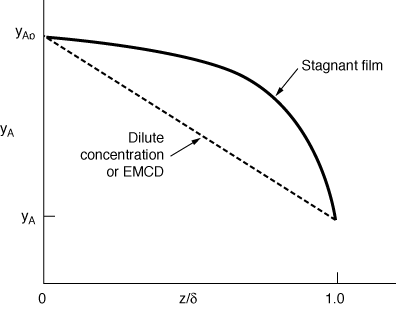
Figure CDE11-3.1
Concentration profiles.

 
   

Step 6: To obtain the molar flux, we differentiate Equation (CDE11-3.9) with respect toz.gif and multiply by cD AB. That is, we combine Equations (CDE11-3.9) and (E11-8.1) to obtain		  
       
   

image 11eq28.gif

(CDE11-3.11)
   

This problem is reworked for diffusion through a stagnant film in the solved example problems on the web solved problems

  
   

If we had assumed diffusion through a stagnant film (Wbz = 0 and BAz = YAWA) rather than dilute concentration or equal molar counter diffusion (BAz = 0), we could use the solution procedure discussed above, starting with

  
       
   

(E11-13)
       
    to arrive at  
       
   

(E11-14)
       
    The intermediate steps are given on the CD-ROM. For the same parameter values as before,  
       
   

(E11-15)
       
    For the case of EMCD  
       
   

 
       
    Net diffusion through a stagnant film is faster.