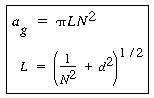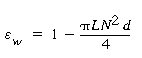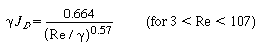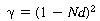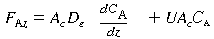Chapter 14: External Diffusion Effects on Heteregeneous Reactions
Professional Reference Shelf
Mass Transfer-Limited Reactions on Metallic Surfaces
|
In this section we develop the design equations and give the mass transfer correlations for two common types of catalytic reactors: the wire screen or catalyst gauze reactor and the monolith reactor. |
|||
A. Catalyst MonolithThe previous discussion in this chapter focused primarily on chemical reactions taking place in packed-bed reactors. However, when a gaseous feed stream contains significant amounts of particulate matter, dust tends to clog the catalyst bed. To process feed streams of this type, parallel-plate reactors (monoliths) are commonly used. Figure R11.1-1 shows a schematic diagram of a monolith reactor. The reacting gas mixture flows between the parallel plates, and the reaction takes place on the surface of the plates. In deriving the design equation we carry out a balance on a differential section of the reactor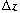 (Figure
R11.1-2). (Figure
R11.1-2). |
|||
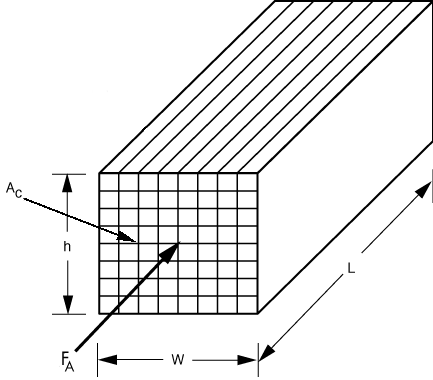
Figure R11.1-1 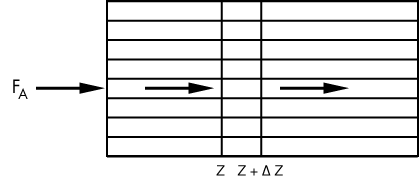
Figure R11.1-2 |
|||
|
Mole balance |

|
(R11.1-1) |
| where am is the catalytic
surface area per unit volume of reactor and A cis
the cross-sectional area normal to the direction of gas flow. The rate of surface reaction is equal to mass flux to the surface. Taking the surface concentration equal to zero for mass transfer-limited reactions gives |
|||
|
|
(R11.1-2) | ||
Substituting Equation (R11.1-2) into (R11.1-1) and taking the
limit as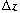 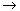 0
yields 0
yields |
|||
|
|
(R11.1-3) | ||
| In terms of volume | |||
|
|
(R11.1-4) | ||
| The surface area per unit volume, a, for n plates is | |||
|
|
(R11.1-5) |
| Typical spacings between the plates are usually between 0.005
and 0.01 m. The length ranges between 0.05 and 0.5 m, and gas velocities
between 5 and 20 m/s are not uncommon. The mass transfer coefficient can be calculated from the correlation |
|||
|
Mass transfer |
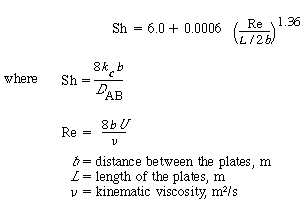
|
(R11.1-6) |
The approximate error in the correlation is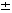 20%.
Other limitations of the correlation can be found in the article just cited
by Arashi et al.1 20%.
Other limitations of the correlation can be found in the article just cited
by Arashi et al.1For no volume change with reaction, Equation (R11.1-4) can be integrated to give |
|||
|
|
(R11.1-7) | ||
|
Ford and Chrysler |
A variation of the monolith reactor has the gas flowing through square (or other shape) channels as shown in Figure R11.1-3. This reactor is also known as a honeycomb reactor. Monolith reactors are used as catalytic afterburners on automobiles and are manufactured by Chrysler and Ford.2
| ||
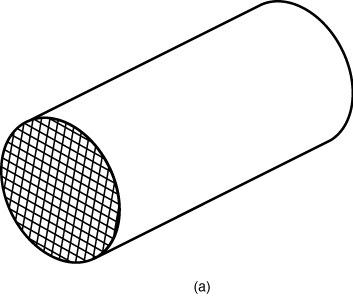
(b) | |||
B. Wire GauzesWire gauzes are commonly used in the oxidation of ammonia and hydrocarbons. A gauze is a series of wire screens, stacked one on top of another (Figure R11.1-4). The wire is typically made out of platinum or a platinum-rhodium alloy. The wire diameter ranges between 0.004 and 0.01 cm.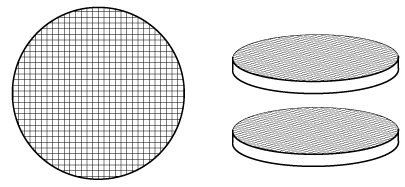
Wire gauzes. As a first approximation, one can assume plug flow through the gauze, in which case the design equation is similar to that for monolith reactors, |
|||
|
Differential form |
|
(R11.1-8) | |
|
where ag = total screen
surface area per total volume of one screen, m2/m3
or in2/in3 The values of ag can be calculated from the equations3
|
|||
| where d = wire diameter, in. N = mesh size, number of wires per linear inch In calculating the volume of the screen, the thickness is taken as twice the wire diameter (i.e., 2d). The porosity can be calculated from the equation |
|||
|
|
|||
| The mass transfer coefficient can be obtained from the correlation for one to three screens, | |||
|
Mass transfer |
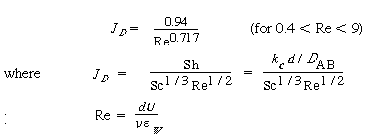
|
(R11.1-9) (R11.1-10) |
| For one to five screens, the correlation is | |||
|
|
(R11.1-11) | ||
where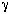 is
the minimum fractional opening of a single screen: is
the minimum fractional opening of a single screen: |
|||
|
|
(R11.1-12) | ||
In the commercial process for the oxidation of ammonia, typical
parameter values are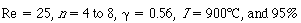 conversion
of ammonia. conversion
of ammonia. |
|||
| When more than one or two screens are necessary, some backmixing takes place. Shimizu et al. 4 account for this backmixing by introducing dispersion in the axial direction: | |||
|
|
(R11.1-13) | ||
|
Too few screens? |
Equation (R11.1-13) is then combined with Equation (R11.1-8) and solved. When dispersion is significant it was shown that, depending on the flow conditions, 33 to 300% more screens were required than predicted by the plug-flow model. |
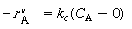
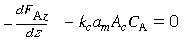
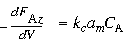
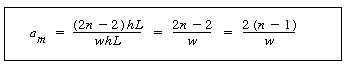
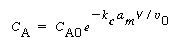

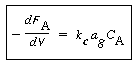
 (volume
per screen)
(volume
per screen)