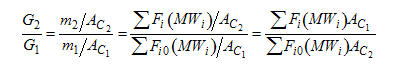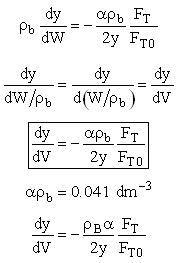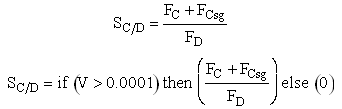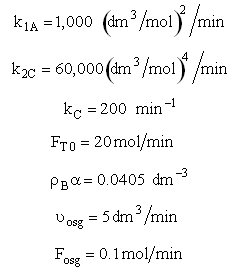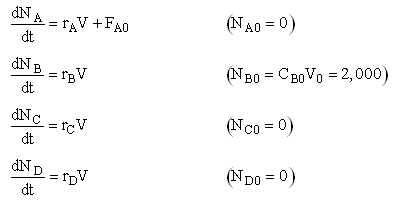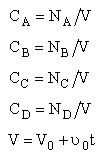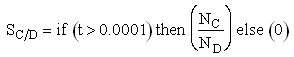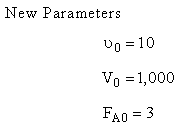6. Multiple Reactions*
Topics
- Types of Multiple Reactions Selectivity and Yield
- Parallel Reactions
- Reactions in Series
- Algorithm for Complex Reactions
- Applications of Algorithm
|
Types of Multiple Reactions Selectivity and Yield |
top |
Types of Multiple Reactions
Use molar flow rates and concentrations; DO NOT use conversion!
There are 4 classes of Multiple Reactions.
1. Parallel Reactions
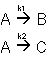
2. Series Reactions
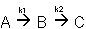
3. Complex Reactions: Series and Parallel aspects combined
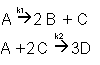
4. Independent Reactions
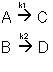
Independent reactions typically occur in the catalytic cracking of crude oil to form gasoline.
Reaction Video: Some multiple reaction systems oscillate, recreating the reactants when certain conditions are met.

What type of reaction is taking place?
Selectivity and Yield (Section 6.1)
There are two types of selectivity and yield: Instantaneous and Overall.

The net rate of disappearance of A
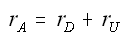
Instantaneous selectivity
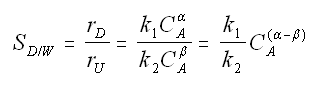
If α > β use high concentration of A. Use PFR.
If α < β use low concentration of A. Use CSTR.

Maximizing the Selectivity - Parallel Reactions
| Series Reactions
(p. 283) |
top |
Example: Series Reaction in a batch reactor
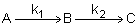
This series reaction could also be written as
Reaction (1)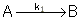 : -r1A=k1CA
: -r1A=k1CA
Reaction (2)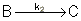 : -r2B=k2CB
: -r2B=k2CB
Mole Balance on every species

Finding the Selectivity
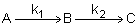 in a CSTR
in a CSTR

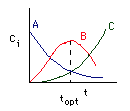
Concentration-Time Trajectories
Schemes for maximizing the selectivity for Van Der Vusse Kinetics
Can be found at the following web site http://www.wits.ac.za/centres/comps/AR/index.htm
| Algorithm for
Complex Reactions |
top |
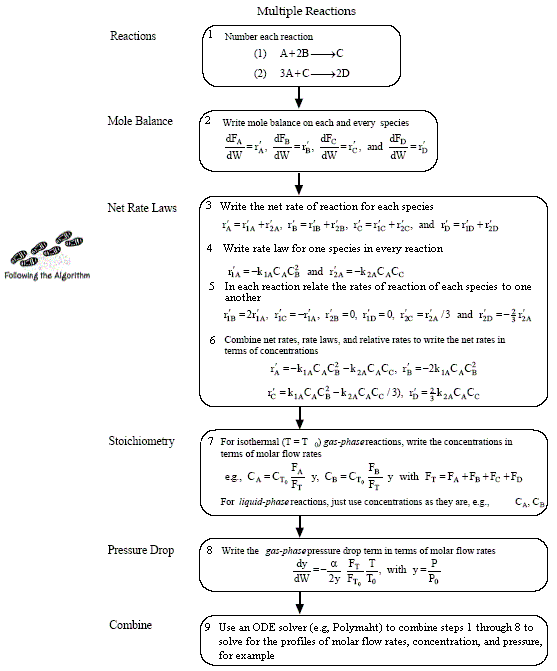
Mole Balances
| Reactor Type |
Gas Phase |
Liquid Phase |
| Batch |
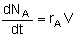 |
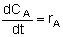 |
| Semibatch |
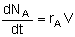 |
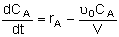 |
| |
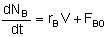 |
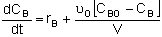 |
| CSTR |
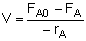 |
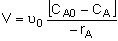 |
| PFR |
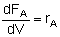 |
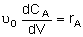 |
| PBR |
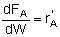 |
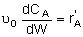
|
Rates
NOTE: The reaction rates in the above mole balances are net rates.
|
The new things for multiple reactions that build on Figure 4-11 and Table 4-6 are
- Number every reaction
- Rate Law for every reaction
- Relative Rates for every reaction
- Net Rates of Reaction
- Number every reaction
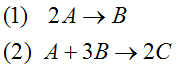
- Rate Laws for every reaction
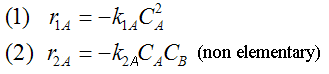
- Relative Rates for each reaction
For a given reaction i
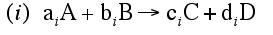
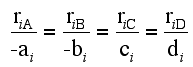
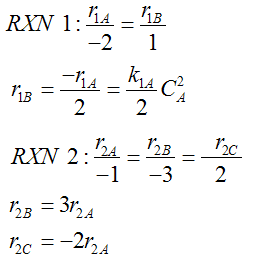
-
Net Rate of Formation for Species A that appears in N reactions,
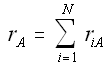
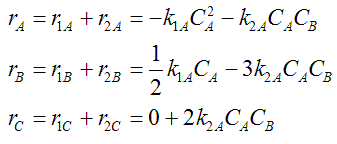
|
Stoichiometry
NOTE: We could use the gas phase mole balance for liquids and then just express the concentration as
Flow CA = FA/υ0
Batch CA = NA/V0
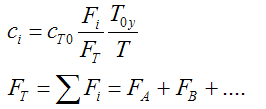

Writing Net Rates of Formation
| Applications of
Algorithm |
top |
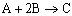 |
(1) |
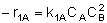 |
NOTE: The specific reaction rate k1A is
defined with respect to species A. |
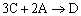 |
(2) |
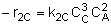 |
NOTE: The specific reaction rate k2C is
defined with respect to species C. |
|
These reactions will be used in the following 5 examples
• Liquid Phase PFR
• Liquid Phase CSTR
• Gas Phase PFR no ΔT
• Gas Phase Membrane Reactor with ΔT
• Liquid Phase Semibatch Reactor
Example A: Liquid Phase PFR
The complex liquid phase reactions follow elementary rate laws
| (1) |
A + 2B → C |
-r1A = k1ACACB2 |
| (2) |
2A + 3C → D |
-r2C = k2CCA2CB3 |
and take place in a PFR. The feed is equal molar in A and B with FA0 = 200 mol/min and the volumetric flow rate is 100 dm3/min. The reaction volume is 50 dm3 and the rate constants are
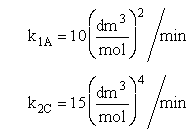
Plot FA, FB, FC, FD and SC/D as a function of V

Multiple Reactions -
Sketch what you think the profile will look like
a priori
Solution
Liquid PFR
Mole Balances
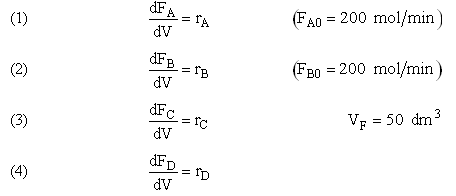
Net Rates
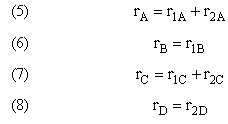
Rate Laws
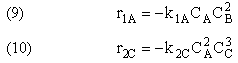
Relative Rates
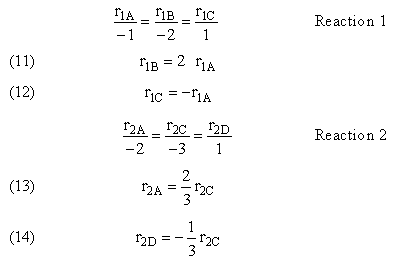
Selectivity
If one were to write SC/D = FC/FD in the Polymath program, Polymath would not execute because at V = 0, FC = 0 resulting in an undefined volume (infinity) at V = 0. To get around this problem we start the calculation 10-4 dm3 from the reactor entrance where FD will note be zero and use the following IF statement.
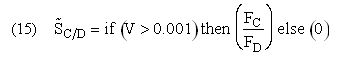
Stoichiometry
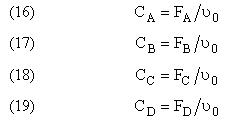
Parameters
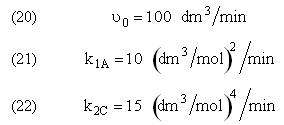
Would you like to see the  results for Example A
results for Example A
Would you like to run  for Example A
for Example A
Example B: Liquid Phase CSTR
Same reactions, rate laws, and rate constants as example A
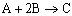 |
(1) |
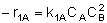 |
NOTE: The specific reaction rate k1A is
defined with respect to species A. |
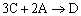 |
(2) |
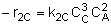 |
NOTE: The specific reaction rate k2C is
defined with respect to species C. |
The complex liquid phase reactions take place in a 2,500 dm3 CSTR. The feed is equal molar in A and B with FA0 = 200 mol/min, the volumetric flow rate is 100 dm3/min and the reaction volume is 50 dm3.
Find the concentrations of A, B, C, and D exiting the reactor along with the exiting selectivity.
Plot FA, FB, FC, FD and SC/D as a function of V
Solution
Liquid CSTR
Mole Balances
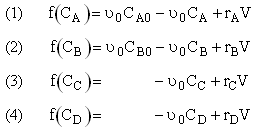
Net Rates
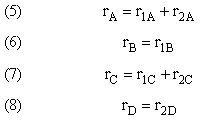
Rate Laws
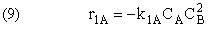
Relative Rates
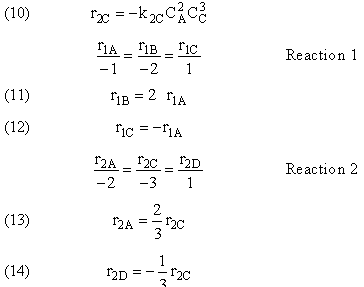
Selectivity
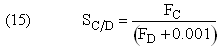
Parameters
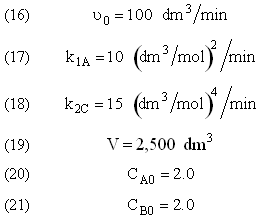
Would you like to see the  results for Example B
results for Example B
Would you like to run  for Example B
for Example B
Example C: Gas Phase PFR, No Pressure Drop
Same reactions and rate laws as previous two examples
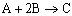 |
(1) |
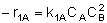 |
NOTE: The specific reaction rate k1A is
defined with respect to species A. |
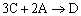 |
(2) |
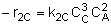 |
NOTE: The specific reaction rate k2C is
defined with respect to species C. |
The complex gas phase reactions take place in a PFR. The feed is equal molar in A and B with FA0 = 10 mol/min and the volumetric flow rate is 100 dm3/min. The reactor volume is 1,000 dm3, there is no pressure drop, the total entering concentration is CT0 = 0.2 mol/dm3 and the rate constants are
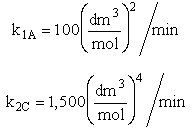
Plot FA, FB, FC, FD and 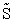 C/D as a function of V
C/D as a function of V
Solution
Gas Phase PFR, No Pressure Drop
Mole Balances
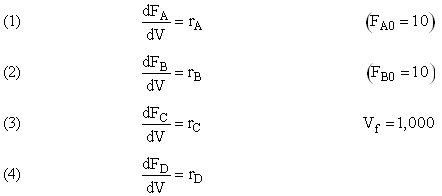
Net Rates
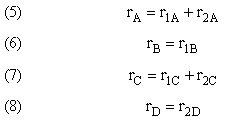
Rate Laws
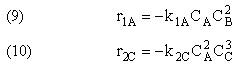
Relative Rates
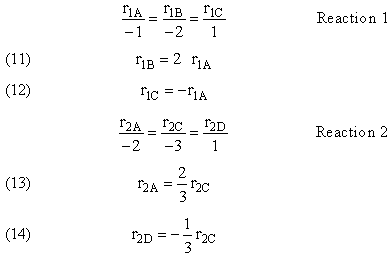
Selectivity
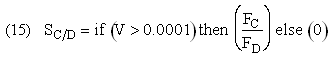
Stoichiometry
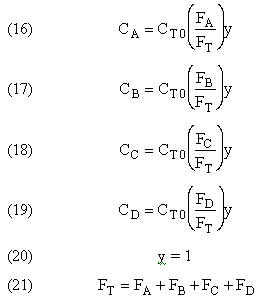
Parameters
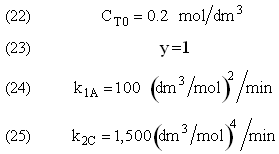
Would you like to see the  results for Example C
results for Example C
Would you like to run  for Example C
for Example C
Example D: Membrane Reactor with Pressure Drop
Same reactions and rate laws as previous two examples
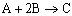 |
(1) |
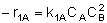 |
NOTE: The specific reaction rate k1A is
defined with respect to species A. |
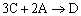 |
(2) |
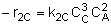 |
NOTE: The specific reaction rate k2C is
defined with respect to species C. |
The complex gas phase reactions take place in a catalytic packed bed with C diffusing out the sides. The feed is equal molar in A and B with FA0 = 10 mol/min and the volumetric flow rate is 100 3/min. The reactor volume is 50 dm3 and the total entering concentration is CT0 = 0.2 mol/dm3. There is pressure drop and entering pressure is 100 atm and the rate constants are
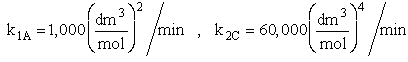
The pressure drop parameter αρb = 0.0405 dm-3
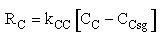
The mass transfer coefficient for C is kcc = 2 min–1
Plot FA, FB, FC, FD and SC/D as a function of V for
(a) Case 1 CCsg = 0
(b) Case 2 CCsg ≠ 0, 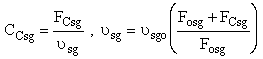
Set Fosg = 0.1 mol/min and vary 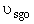
(5 < 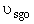 < 10,000)
< 10,000)
Are there a set of conditions whereby (CCsg < CC) and RC changes sign and Species C diffuses back into the membrane reactor near the exit? Run the Polymath program when αρb = 0 and compare RC with the base case when there IS pressure drop (αρb = 0.0405 dm-3)
Solution
Gas Phase Multiple Reactions in a Catalytic Packed Bed Membrane Reactor with Pressure Drop
Mole Balances
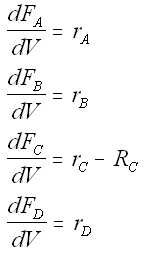
We also need to account for the molar rate desired product C leaving in the sweep gas FCsg
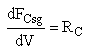
Rate Laws
- Net rates, rate laws and relative rates same as Liquid and Gas Phase PFR and Liquid Phase CSTR.
- Transport Law
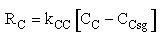
Case 1 Large sweep gas velocity
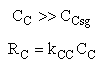
Case 2 Moderate to small sweep gas velocity
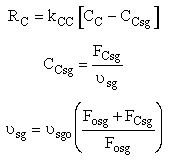
Vary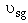 to see changes in profiles
to see changes in profiles
Case 2A Pressure Drop
Case 2B No Pressure Drop
Stoichiometry
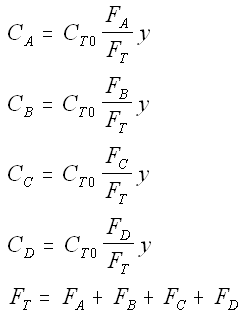
We need to reconsider our pressure drop equation when one or more species diffuse out of the reactor. Recall the pressure drop equation is
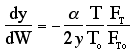
with
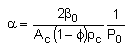
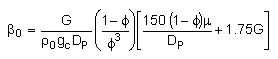
Warning!!
When mass diffuses out of a membrane reactor as there will be a decrease in the superficial mass flow rate 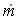 and hence G. To account for this decrease in calculating our pressure drop parameter , we will take the ratio of the superficial mass velocity at any point in the reactor to the superficial mass velocity at the entrance to the reactor. The superficial mass flow rates can be obtained by multiplying the species molar flow rates, Fi, by their respective molecular weights, MWi, and then summing over all species and hence G. To account for this decrease in calculating our pressure drop parameter , we will take the ratio of the superficial mass velocity at any point in the reactor to the superficial mass velocity at the entrance to the reactor. The superficial mass flow rates can be obtained by multiplying the species molar flow rates, Fi, by their respective molecular weights, MWi, and then summing over all species
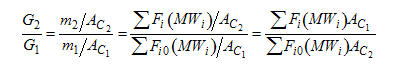
Because the smallest molecule is the one diffusing out and has the lowest molecular weight, we will neglect the changes in the mass flow rate down the reactor and will take as a first approximation.
|
Isothermal (T = T0) and multiply both sides of the pressure drop equation by the bulk density, ρb
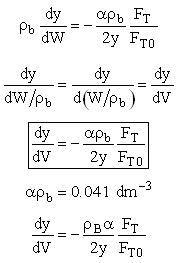
Selectivity
Need to include C collected from sweep gas
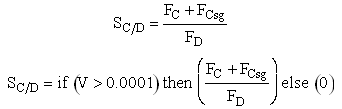
Parameters
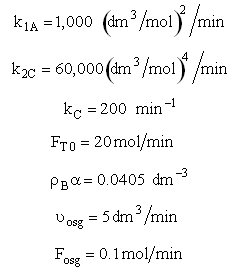
Would you like to see the  results for Example D
results for Example D
Would you like to run  for Example D
for Example D
Example E: Liquid Semibatch
Same reactions, rate laws, and rate constants as example A
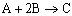 |
(1) |
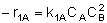 |
NOTE: The specific reaction rate k1A is
defined with respect to species A. |
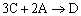 |
(2) |
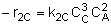 |
NOTE: The specific reaction rate k2C is
defined with respect to species C. |
The complex liquid phase reactions take place in a semibatch reactor where A is fed to B with FA0 = 3 mol/min. The volumetric flow rate is 10 dm3/min and the initial reactor volume is 1,000 dm3.
The maximum volume is 2,000 dm3 and CA0 = 0.3 mol/dm3 and CB0 = 0.2 mol/dm3. Plot CA, CB, CC, CD and SC/D as a function of time.
Solution
Liquid Phase Multiple Reactions in a Semibatch Reactor
Mole Balances
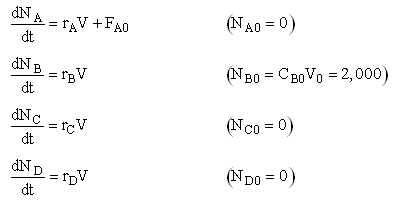
Net Rates, Rate Laws and relative rates – are the same as Liquid and Gas Phase PFR and Liquid Phase CSTR.
Stoichiometry
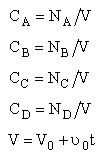
Selectivity
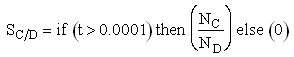
Parameters
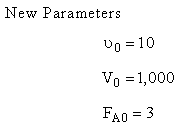
Would you like to see the  results for Example E
results for Example E
Would you like to run  for Example E
for Example E

What's wrong with this solution?

ODE Solver Algorithm

Object Assessment of Chapter 6
 Explore the cobra bites web module
Explore the cobra bites web module
*
All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering
.
top
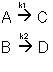
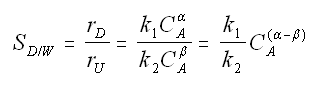
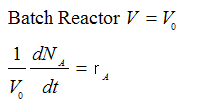
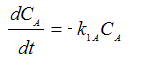
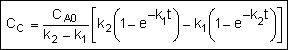

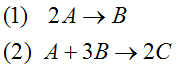
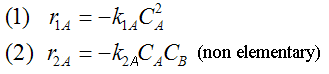
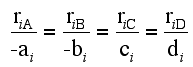
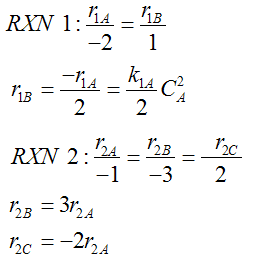
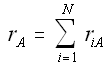
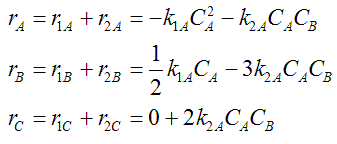
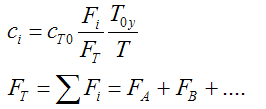
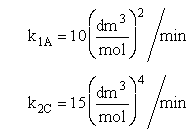
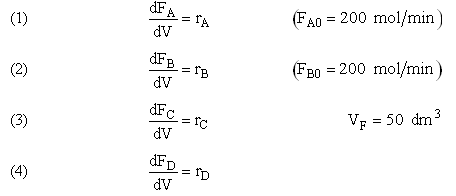
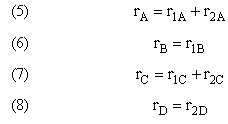
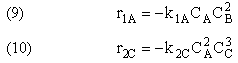
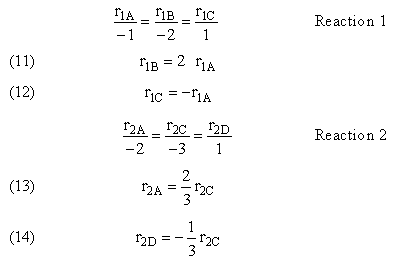
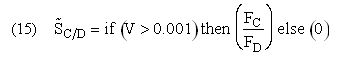
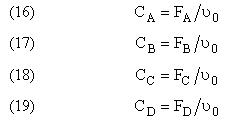
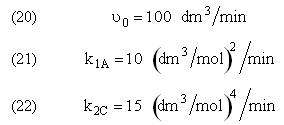

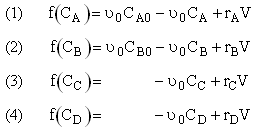
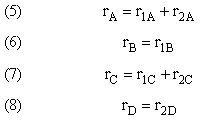
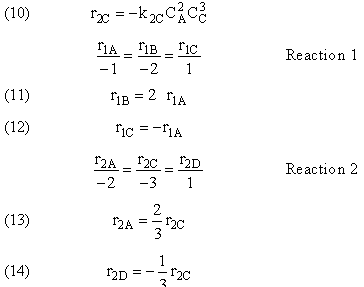
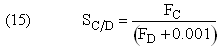
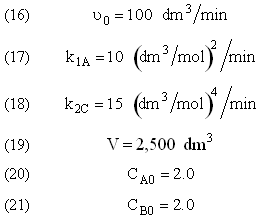
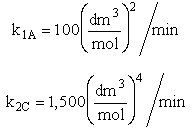
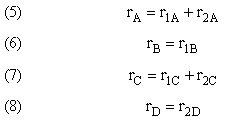
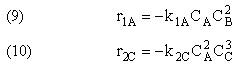
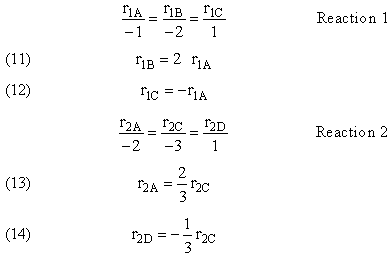
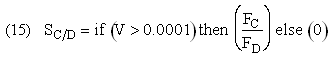
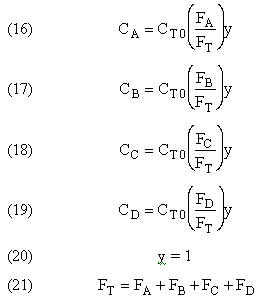
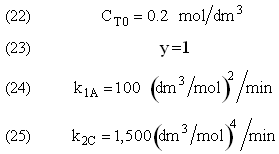
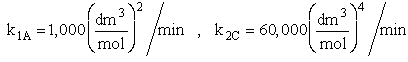
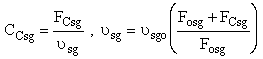
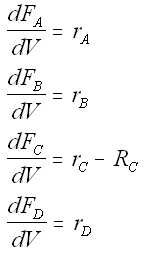
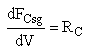
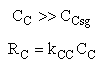
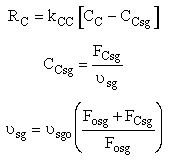
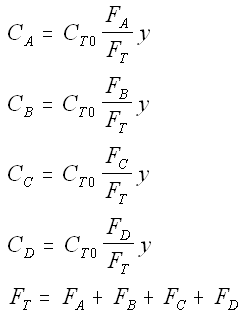
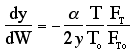
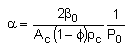
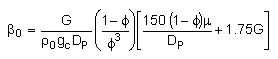

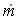 and hence G. To account for this decrease in calculating our pressure drop parameter , we will take the ratio of the superficial mass velocity at any point in the reactor to the superficial mass velocity at the entrance to the reactor. The superficial mass flow rates can be obtained by multiplying the species molar flow rates, Fi, by their respective molecular weights, MWi, and then summing over all species
and hence G. To account for this decrease in calculating our pressure drop parameter , we will take the ratio of the superficial mass velocity at any point in the reactor to the superficial mass velocity at the entrance to the reactor. The superficial mass flow rates can be obtained by multiplying the species molar flow rates, Fi, by their respective molecular weights, MWi, and then summing over all species