AEROSOL REACTORS
Procedure
Step 1. Find the rate of formation of g-mers by summing at g-mer formation from g = 2 to a very large number G to obtain
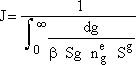
Step 2. Define H(g) = ln
and
expand H(g) in a Taylor series about g*
Step 3. Change variables to let
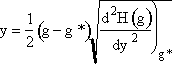
and approximate the lower limit of integration, a, by ¥ and use the definition of the probability integral to obtain
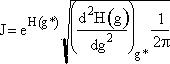
Step 4. Find the critical nucleus size
Step 5. Evaluate terms in
H(g*) and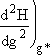 
then
neglect 
w.r.t. 
to obtain
Step 6. Evaluate A at g* to obtain
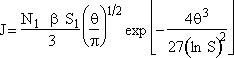
Step 7. Simplify the pre-exponential to obtain
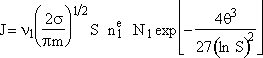
Step 8. Evaluate N1 and recall
to obtain
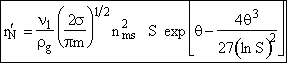
End result.
Nucleation Kinetics
We will now derive the following
equation for the nucleation rate 
[See Girshick and Chiu (1990)]
1. Calculate the rate of formation of g-mers. Jg
From kinetic collision theory we have
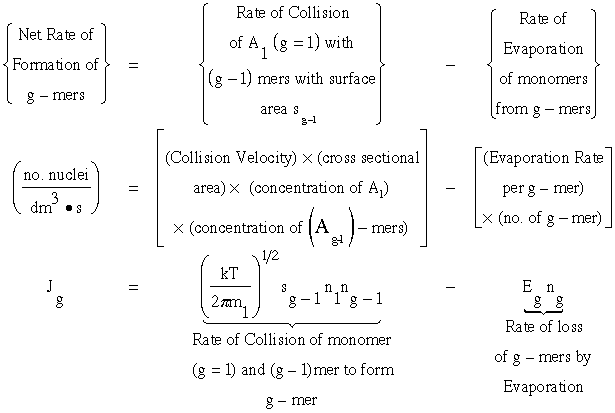(1)
Recall that the collision velocity is (Um/4)
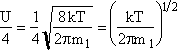
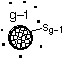
where n1 is the monomer concentration (molecules/dm3), ng-1 is the concentration of (g-1) mers (number/dm3), sg-1 is the surface area (dm2) of the (g-1)-mer and Eg the evaporation rate constant for the g-mers, (seconds1).
At equilibrium Jg
= 0 and 
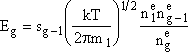
n1 is the concentration of monomers, 
is
the equilibrium concentration of monomers (molecules/dm3), and 
is the equilibrium
concentration of g-mers (number/dm3)
Let 
(2)
At steady state the rates of formation of g-mers are the same J1 = J2 = … Jg, rearranging
(3)
We will now evaluate Equation (3) for different values of g, starting with g=2
g=2
, 
Dividing by S
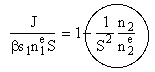(4)
g=3
, 
(5)
|
We continue writing the equations analogous to equation (4) and (5) up to some arbitrary value of g, g = G |
. . . . |
(6)
When we sum all these equations (4) through (6), we see all
terms on the right hand side cancel out (e.g. circled terms in Equations (4)
and (5) when added) except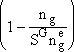 
of
the rhs
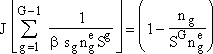(7)
For large G and S > 1, we can neglect second term on right hand side so that r.h.s. becomes unity.
Next we take the reciprocal and sum over all gmers and then for large G we can replace the summation å by an integral ò.
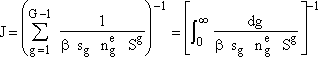(8)
(9)
where
(10)
(11)
We observe that this function will go through a minimum and consequently the first derivative will be zero
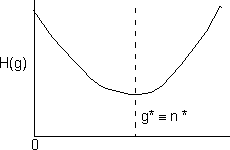
This minimum corresponds to the critical g-mer size. Particles larger than the critical size n* are stable while those smaller than n* are not.
Returning to the equation for the rate of formation of a g-mer,
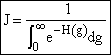(9)
We focus on evaluating the denominator, D,
(11A)
2. First we use a Taylor series to expand H(g) about the critical size g*
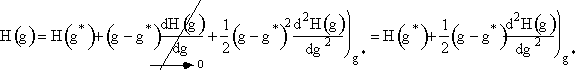(12)
Using Eqn. (12) to substitute for H(g) in the denominator D.
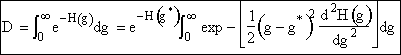(13)
We now want to evaluate the integral in D.
3. We now consider the lower limit of the integration
when g = 0 then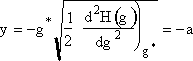 
, a constant
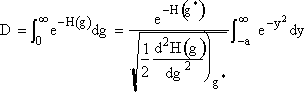(14)
Now let’s look at a typical value of the lower limit of integration a.
(
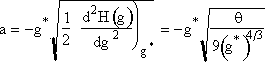from Eqn. 27)
Even choosing conservative values for q (q=18) and g* (g*=1000) we see a is a large negative number the order of (10)
This value of the lower limit (a = 10, a = 10)
is very large for the function we have, 
,
so therefore we can essentially replace it with minus infinity. Actually any
value greater than a=3 is essentially equivalent to setting the lower limit
at ¥. Therefore set a » ¥
and we obtain the probability integral
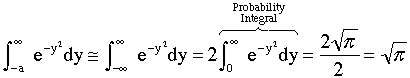(15)
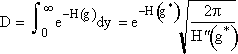
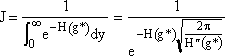
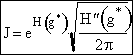(16)
where
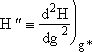
Before we can evaluate H²(g*) we need to find the critical radius.
4. Finding the critical nucleus size g*
(17)
where N1 is a normalizing factor to be determined later.
(18)
where
We previously showed that DG goes through a maximum at g*
(19)
As previously noted, particles of size greater than the critical size g* are stable. Particles larger than g* will grow while particles small than g* are not stable.
Expanding H(g)
(20)
(21)
Applying Eqn. (21) at stable equilibrium S=1, for the kinetic theory derivation equation (7) becomes
(22)
The number of gmers per unit volume at equilibrium is given by a Boltzmann distribution
(23)
where DG(g) is the Gibbs free energy of g-mer formation in the equilibrium state. N1 is a normalization factor
for g = 1
Equation (21) becomes
(24)
or
(25)
5. Evaluating Terms in H(g)
Evaluating H(g*) and d2H(g*)/dg2
Substituting Eqns. (21, 22, and 23) into Eqn. (20)
(26)
(16)
Differentiating Equation (26) twice wrt g
Since g > 10 we neglect g2 wrt 
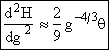(27)
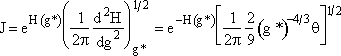
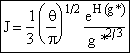(28)
Evaluating exp [H(g*)]
Replacing H(g*) in the exponential using Eqn. (10).
(29)
(30)
Combining Equations (28) and (30)
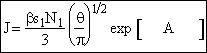(31)
where
6. Evaluate A at g*
Recall g* = 
(32)
Substituting Eqn. (32) back into Eqn. (31)
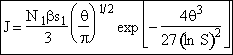(33)
7. Simplify the Pre-exponential
We now will simplify the pre-exponential term.
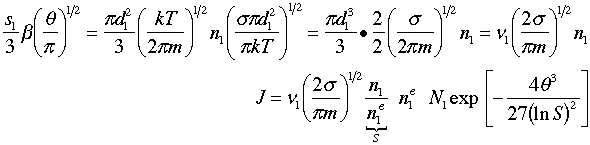(34)
(35)
8. We now need to eliminate N1
Recall N1,
where 
, the concentration of monomers
at saturation. Therefore the rate of formation of nuclei per unit volume (number
of nuclei/s/dm3) is
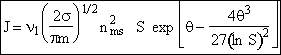(36)
Rate of loss of monomers to form nuclei per unit mass of gas is
(37)
This is the result we have been looking for