Chapter 4: Stoichiometry

Writing -r_A Solely as a Function of X.

Write the rate law for the elementary liquid phase reaction

solely in terms of conversion. The feed to the batch reactor is equal molar A and B with C_A0 = 2 mol/dm³ and k_A= .01 (dm³/mol)⁴1/s.

Hint 1: What is the rate law?

(a) $-r_{A} = k_{A}C_{A}{C_{B}}^{\frac{2}{3}}$

(b) $-r_{A} = k_{A}C_{A}{C_{B}}$

(c) $-r_{A} = k_{A}{C_{A}}^3{C_{B}}^2$

Hint 2: What is the concentration of A?

(a) $C_{A} = C_{A0}(1-x)$

(b) $C_{A} = C_{A0}(2-x)$

(c) $C_{A} = C_{A0}(1-3x)$

Hint 3: What is the concentration of B?

(a) $C_{B} = C_{A0}(1-\frac{2}{3}x)$

(b) $C_{B} = C_{A0}(\frac{2}{3} - \frac{2}{3}x)$

(c) $C_{B} = C_{A0}(1-2x)$

Full Solution

Hint 1

What is the rate law?

The reaction is elementary so what happens to the coefficients from the reaction?

Back to Problem

Hint 2

What is the concentration of A?

Liquid phase, v = v_o (no volume change)

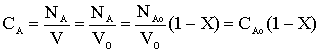
Back to Problem

Hint 3

What is the concentration of B?

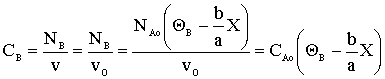
What is Θ_B?

Equal molar

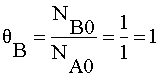
Species A is the limiting reactant because the feed is equal molar in A and B, and two moles of B consumes 3 moles of A.

Back to Problem

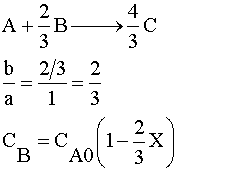
Solution

Write the rate law for the elementary liquid phase reaction

solely in terms of conversion. The feed to the batch reactor is equal molar A and B with C_A0 = 2 mol/dm³ and k_A= .01 (dm³/mol)⁴1/s.

1) Rate Law: -r_A=kC³_AC²_B

2) Stoichiometry:

Species A

Liquid phase, v = v_o (no volume change)

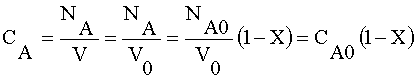
Species B

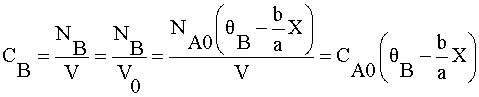
What is Θ_B?

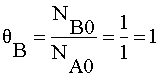
Species A is the limiting reactant because the feed is equal molar in A and B, and two moles of B consumes 3 moles of A.

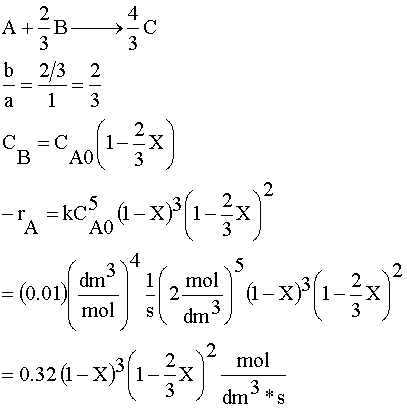
We now have -r_A=f(X) and can size reactors or determine batch reaction times.

Back to Chapter 4

Elements of
Chemical Reaction Engineering
6th Edition

Home

Essentials of
Chemical Reaction Engineering
Second Edition

By Chapter Hide

By Concept Hide

U of M Hide

Chapter 4: Stoichiometry

Writing -r_A Solely as a Function of X.

(a) $-r_{A} = k_{A}C_{A}{C_{B}}^{\frac{2}{3}}$

(b) $-r_{A} = k_{A}C_{A}{C_{B}}$

(c) $-r_{A} = k_{A}{C_{A}}^3{C_{B}}^2$

(a) $C_{A} = C_{A0}(1-x)$

(b) $C_{A} = C_{A0}(2-x)$

(c) $C_{A} = C_{A0}(1-3x)$

(a) $C_{B} = C_{A0}(1-\frac{2}{3}x)$

(b) $C_{B} = C_{A0}(\frac{2}{3} - \frac{2}{3}x)$

(c) $C_{B} = C_{A0}(1-2x)$

By Chapter Hide

By Concept Hide

U of M Hide

Chapter 4: Stoichiometry

Writing -rA Solely as a Function of X.

Writing -r_A Solely as a Function of X.