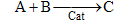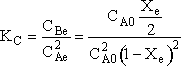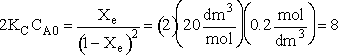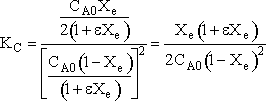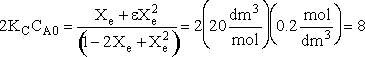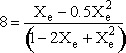Chapter 4: Stoichiometry
Rationale For Chapter 4
In chapter 2 we saw that if we had –rA as a function of X, [–rA= f(X)] we could size many reactors and reactor sequences and systems.

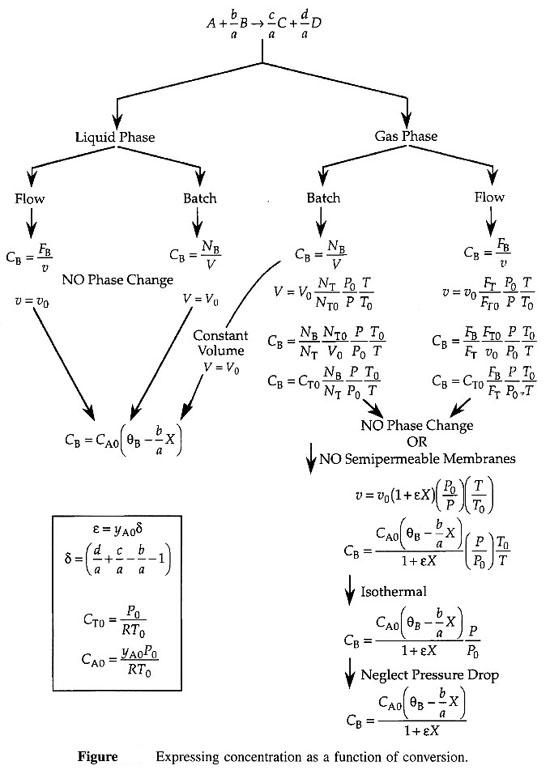
How do we obtain –rA = f(X)? We do this in two steps 1. Part 1 - Chapter 3 Rate Law – Find the rate as a function of concentration, –rA = k fn (CA, CB …) 2. Part 2 - Chapter 4 Stoichiometry – Find the concentration as a function of conversion CA = g(X) Combine Part 1 and Part 2 to get -rA=f(X) |
Stoichiometry
We shall set up Stoichiometric Tables using A as our basis of calculation
in the following reaction. We will use the stoichiometric tables to express
the concentration as a function of conversion. We will combine Ci
= f(X) with the appropriate rate law to obtain -rA = f(X).
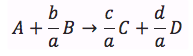
Topics
| Batch System Stoichiometric Table | top |
| Species | Symbol | Initial | Change | Remaining |
|---|---|---|---|---|
| A | A | |||
| B | B | |||
| C | C | |||
| D | D | |||
| Inert | I | ________ |
------- | ____________ |
| and |
Concentration -- Batch System: |
Constant Volume Batch:
|
Note: if the reaction occurs in the liquid phase or if a gas phase reaction occurs in a rigid (e.g., steel) batch reactor |
|
| Then | |
| etc. | |
if ![]() then
then
|
| Flow System Stoichiometric Table | top |
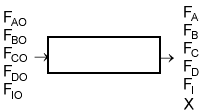 |
||||
| Species | Symbol | Reactor Feed | Change | Reactor Effluent |
|---|---|---|---|---|
| A | A | |||
| B | B | |||
| C | C | |||
| D | D | |||
| Inert | I | ________ |
------- | ____________ |
| and |
Concentration -- Flow System:
|
Liquid Phase Flow System:
|
|
|
If the rate of reaction were -rA = kCACB then
we would have ![]()
This
gives us -rA = f(X). Consequently, we can use the methods
discussed in Chapter 2 to size a large number of reactors, either alone
or in series.
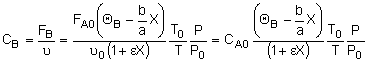 |
|
etc. Again, these equations give us information about -rA = f(X), which we can use to size reactors.
then |
|
|
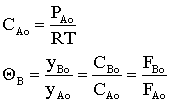
Calculating the equilibrium conversion for gas phase reaction
Consider the following elementary reaction with KC and = 20 dm3/mol and CA0 = 0.2 mol/dm3. Pure A fed. Calculate the equilibrium conversion, Xe, for both a batch reactor and a flow reactor.
Solution
At equilibrium
Stoichiometry
Batch
Species Initial Change Remaining A NA0 -NA0X NA = NA0(1-X) B 0 +NA0X/2 NB = NA0X/2 NT0 = NA0 NT = NA0 - NA0X/2 Constant Volume V = V0
Solving
Flow
Species Fed Change Remaining A FA0 -FA0X FA = F A0(1-X) B 0 +FA0X/2 FB = F A0X/2 FT0 = F A0 FT = F A0 - F A0X/2
Recall
* All chapter references are for the 1st Edition of the text Essentials of Chemical Reaction Engineering .
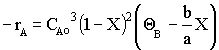 Constant Volume Batch
Constant Volume Batch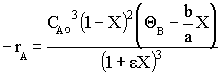 Flow Gas Phase
Flow Gas Phase