Chapter 6: Isothermal Reactor Design: Molar Flow Rates

Gas Phase PFR

Problem:

The elementary irreversible gas phase reaction 2A -> B is carried out isothermally with no pressure drop in a PFR.

Given:

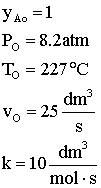
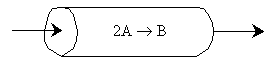
Use measures other than conversion to plot molar flow rates of A and B down the reactor.

Hint 1: What are the mole balances on A and B and the rate law?

mole balances on A ?

(a) $\frac{dF_{A}}{dV} = 2r_{A}$

(b) $\frac{dF_{A}}{dV} = -2r_{A}$

(c) $\frac{dF_{A}}{dV} = -r_{A}$

(d) $\frac{dF_{A}}{dV} = r_{A}$

mole balances on B ?

(a) $\frac{dF_{B}}{dV} = r_{A}$

(b) $\frac{dF_{B}}{dV} = -2r_{A}$

(c) $\frac{dF_{B}}{dV} = \frac{-r_{A}}{2}$

(d) $\frac{dF_{B}}{dV} = \frac{r_{A}}{2}$

rate law ?

(a) $r_{A} = -k{C_{A}}^2$

(b) $r_{A} = k{C_{A}}^2$

(c) $r_{A} = kC_{A}$

Hint 2: What are the concentrations of A and B?

(a) $C_{A} = C_{T0}\frac{F_{A}}{F_{B}}p\frac{T_{0}}{T}$

(b) $C_{A} = C_{T0}\frac{F_{A}}{F_{A}+F_{B}}p\frac{T_{0}}{T}$

Hint 3: What is the rate of formation of B?

(a) $r_{B} = \frac{1}{2}C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

(b) $r_{B} = -2C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

(c) $r_{B} = -\frac{1}{2}C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

Hint 4: What are the combined mole balance, rate law and stoichiometry?

(a) $\frac{dF_{A}}{dV} = k_{A}C_{T0}\frac{F_{A}}{F_{A}+F_{B}}$

(b) $\frac{dF_{A}}{dV} = -k_{A}C_{T0}\frac{F_{A}}{F_{A}+F_{B}}$

Hint 5: What is the polymath program?

Full Solution

Hint 1 - Mole Balances and Rate Law

Mole Balances

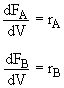
Rate Law

Back to Hints

Back to Problem

Hint 2 - Concentrations

Stoichiometry

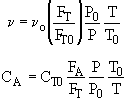
For Isothermal and No DP

Back to Hints

Back to Problem

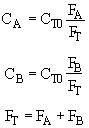
Hint 3 - Rate of Formation of B

$\textrm{For } A + \frac{b}{a}B \rightarrow \frac{c}{a}C + \frac{d}{a}D$

$\frac{r_{A}}{-a} = \frac{r_{B}}{-b} = \frac{r_{C}}{c} = \frac{r_{D}}{d}$

$\textrm{For } 2A \rightarrow B$

$\frac{r_{A}}{(-2)} = \frac{r_{B}}{(1)}$

$r_{B} = \frac{1}{2}(-r_{A}) = \frac{k_{A}}{2}{C_{A}}^2$

Back to Hints

Back to Problem

Hint 4 - Combined Mole Balances, Rate Law and Stoichiometry

Combine

Back to Hints

Back to Problem

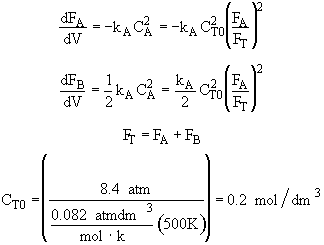
Hint 5 - Polymath Code

[Note: To=227C=500K]

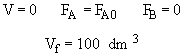
Use Polymath to solve

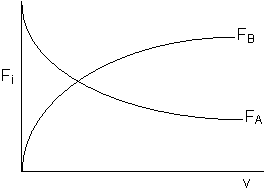
One can back calculate X

See the Polymath Solution Below

POLYMATH 5.0 Results

01-19-2001

Calculated values of the DEQ variables

Variable	initial value	minimal value	maximal value	final value
V	0	0	25.	25.
Fa	5	1.0026274	5	1.0026274
Fb	0	0	1.9986863	1.9986863
Cto	0.2	0.2	0.2	0.2
ka	10	10	10	10
Ft	5	3.0013137	5	3.0013137
x	0	0	0.7994745	0.7994745

ODE Report (RKF45)

Differential equations as entered by the user

[1] d(Fa)/d(V) = -ka*Cto^2*(Fa/Ft)^2

[2] d(Fb)/d(V) = 0.5*ka*Cto^2*(Fa/Ft)^2

Explicit equations as entered by the user

[1] Cto = 0.2

[2] ka = 10

[3] Ft = Fa+Fb

[4] x = (5-Fa)/5

Back to Hints

Back to Problem

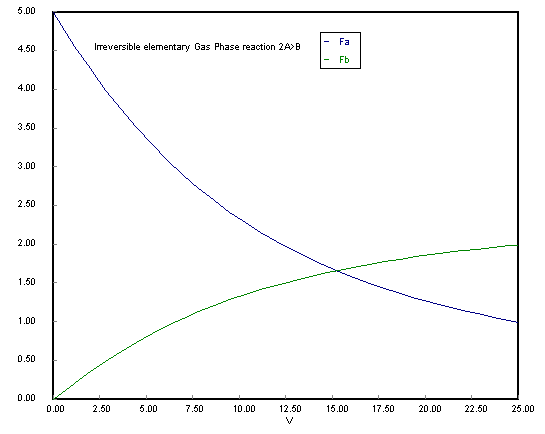
Full Solution

Mole Balances

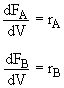
Rate Law

Stoichiometry

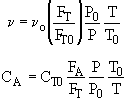
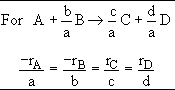
For 2A->B

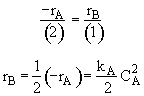
For Isothermal and No DP

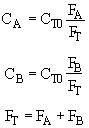
Combine

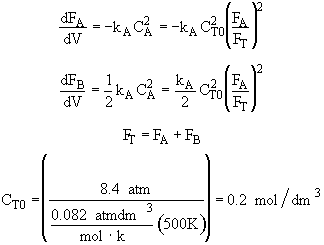
[Note: To=227C=500K]

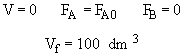
Use Polymath to solve

One can back calculate X

See the Polymath Solution Below

POLYMATH 5.0 Results

01-19-2001

Calculated values of the DEQ variables

Variable	initial value	minimal value	maximal value	final value
V	0	0	25.	25.
Fa	5	1.0026274	5	1.0026274
Fb	0	0	1.9986863	1.9986863
Cto	0.2	0.2	0.2	0.2
ka	10	10	10	10
Ft	5	3.0013137	5	3.0013137
x	0	0	0.7994745	0.7994745

ODE Report (RKF45)

Differential equations as entered by the user

[1] d(Fa)/d(V) = -ka*Cto^2*(Fa/Ft)^2

[2] d(Fb)/d(V) = 0.5*ka*Cto^2*(Fa/Ft)^2

Explicit equations as entered by the user

[1] Cto = 0.2

[2] ka = 10

[3] Ft = Fa+Fb

[4] x = (5-Fa)/5

Back to Chapter 6

Elements of
Chemical Reaction Engineering
6th Edition

Home

Essentials of
Chemical Reaction Engineering
Second Edition

By Chapter Hide

By Concept Hide

U of M Hide

Chapter 6: Isothermal Reactor Design: Molar Flow Rates

Gas Phase PFR

(a) $\frac{dF_{A}}{dV} = 2r_{A}$

(b) $\frac{dF_{A}}{dV} = -2r_{A}$

(c) $\frac{dF_{A}}{dV} = -r_{A}$

(d) $\frac{dF_{A}}{dV} = r_{A}$

(a) $\frac{dF_{B}}{dV} = r_{A}$

(b) $\frac{dF_{B}}{dV} = -2r_{A}$

(c) $\frac{dF_{B}}{dV} = \frac{-r_{A}}{2}$

(d) $\frac{dF_{B}}{dV} = \frac{r_{A}}{2}$

(a) $r_{A} = -k{C_{A}}^2$

(b) $r_{A} = k{C_{A}}^2$

(c) $r_{A} = kC_{A}$

(a) $C_{A} = C_{T0}\frac{F_{A}}{F_{B}}p\frac{T_{0}}{T}$

(b) $C_{A} = C_{T0}\frac{F_{A}}{F_{A}+F_{B}}p\frac{T_{0}}{T}$

(a) $r_{B} = \frac{1}{2}C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

(b) $r_{B} = -2C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

(c) $r_{B} = -\frac{1}{2}C_{T0}\frac{F_{B}}{F_{T}}p\frac{T_{0}}{T}$

(a) $\frac{dF_{A}}{dV} = k_{A}C_{T0}\frac{F_{A}}{F_{A}+F_{B}}$

(b) $\frac{dF_{A}}{dV} = -k_{A}C_{T0}\frac{F_{A}}{F_{A}+F_{B}}$

Hint 1 - Mole Balances and Rate Law

Hint 2 - Concentrations

Hint 3 - Rate of Formation of B

Hint 4 - Combined Mole Balances, Rate Law and Stoichiometry

Hint 5 - Polymath Code

Full Solution