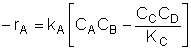Chapter 6: Isothermal Reactor Design: Molar Flow Rates

Topics

1. Measures Other Than Conversion
2. Membrane Reactors
3. Semibatch Reactors

Measures Other Than Conversion	top

Uses:

A. Membrane reactors
B. Multiple reaction

Liquids: Use concentrations, i.e. C_A

                                                                      

1. For the elementary liquid phase reaction carried out in a CSTR, where V, v_o, C_Ao, k, and K_c are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry are:

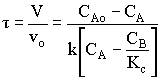
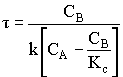
There are two equations, two unknowns, C_A and C_B

Gases: Use Molar Flow Rates, I.E. F_i

                                                                

                                                         

                                          

2. If the above reaction, ,carried out in the gas phase in a PFR, where V, v_o,C_Ao,k, and K_c are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry yield, for isothermal operation (T=To) and no pressure drop (DP=0) are:

  

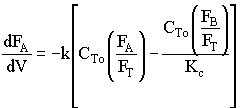
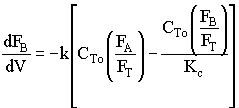
Use Polymath to plot F_A and F_B down the length of the reactor.

Microreactors

For isothermal microreactors, we use the same equations as a PFR as long as the flow is not laminar. If the flow is laminar, we must use the techniques discussed in chapter 13. See example 4.8 of the text.

Membrane Reactors	top

Membrane reactors can be used to achieve conversions greater than the original equilibrium value. These higher conversions are the result of Le Chatelier's Principle; you can remove one of the reaction products and drive the reaction to the right. To accomplish this, a membrane that is permeable to that reaction product, but is impermeable to all other species, is placed around the reacting mixture.

Example: The following reaction is to be carried out isothermally in a membrane reactor with no pressure drop. The membrane is permeable to Product C, but it is impermeable to all other species.

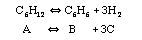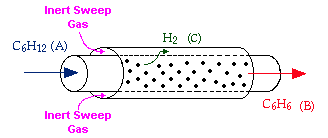For membrane reactors, we cannot use conversion. We have to work in terms of the molar flow rates F_A, F_B, F_C.               

Polymath Program

Mole Balances

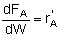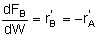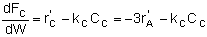Rate Laws
Stoichiometry Isothermal, no pressure drop

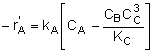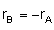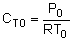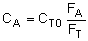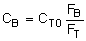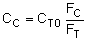Combine	Polymath will combine for you-- Thanks Polymath...you rock!
Parameters
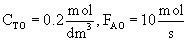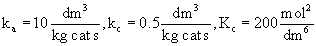Solve	Polymath

Below are links to example problems dealing with membrane reactors. You could also use these problems as self tests.

Semibatch Reactors	top

Semibatch reactors can be very effective in maximizing selectivity in liquid phase reactions.

The reactant that starts in the reactor is always the limiting reactant.

Three Forms of the Mole Balance Applied to Semibatch Reactors:

1. Molar Basis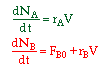
2. Concentration Basis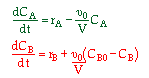
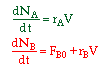3. Conversion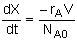

For constant molar feed:
For constant density:

Use the algorithm to solve the remainder of the problem.

Example: Elementary Irreversible Reaction

Consider the following irreversible elementary reaction:

-r_A = kC_AC_B

The combined mole balance, rate law, and stoichiometry may be written in terms of number of moles, conversion, and/or concentration:

Conversion	Concentration	Number of Moles

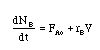Polymath Equations:

Conversion	Concentration	Moles
d(X)/d(t) = -ra*V/Nao	d(Ca)/d(t) = ra - (Ca*vo)/V	d(Na)/d(t) = ra*V
ra = -k*Ca*Cb	d(Cb)/d(t) = rb + ((Cbo-Cb)*vo)/V	d(Nb)/d(t) = rb*V + Fbo
Ca = Nao*(1 - X)/V	ra = -k*Ca*Cb	ra = -k*Ca*Cb
Cb = (Nbi + Fbo*t - Nao*X)/V	rb = ra	rb = ra
V = Vo + vo*t	V = Vo + vo*t	V = Vo + vo*t
Vo = 100	Vo = 100	Vo = 100
vo = 2	vo = 2	vo = 2
Nao = 100	Fbo = 5	Fbo = 5
Fbo = 5	Nao = 100	Ca = Na/V
Nbi = 0	Cbo = Fbo/vo	Cb = Nb/V
k = 0.1	k = 0.01	k = 0.01
	Na = Ca*V
	X = (Nao-Na)/Nao

Polymath Screenshots:

Conversion	Concentration
Polymath Equations	Polymath Equations
SummaryTable	Summary Table
Conversion vs.Time	Conversion vs.Time
Concentration vs.Time	Concentration vs.Time
Volume vs.Time	Volume vs.Time

Equilibrium Conversion in Semibatch Reactors with Reversible Reactions

Consider the following reversible reaction:

Everything is the same as for the irreversible case, except for the rate law:

Where:

At equilibrium, -r_A=0, then

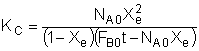
See Also: 

Polymath Book Problems

A. Chapter 6 PBR ODE Solver Algorithm

PFR with Pressure Drop

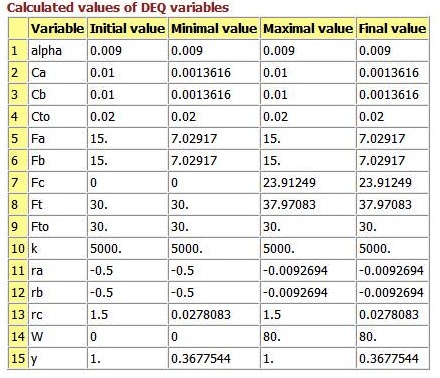
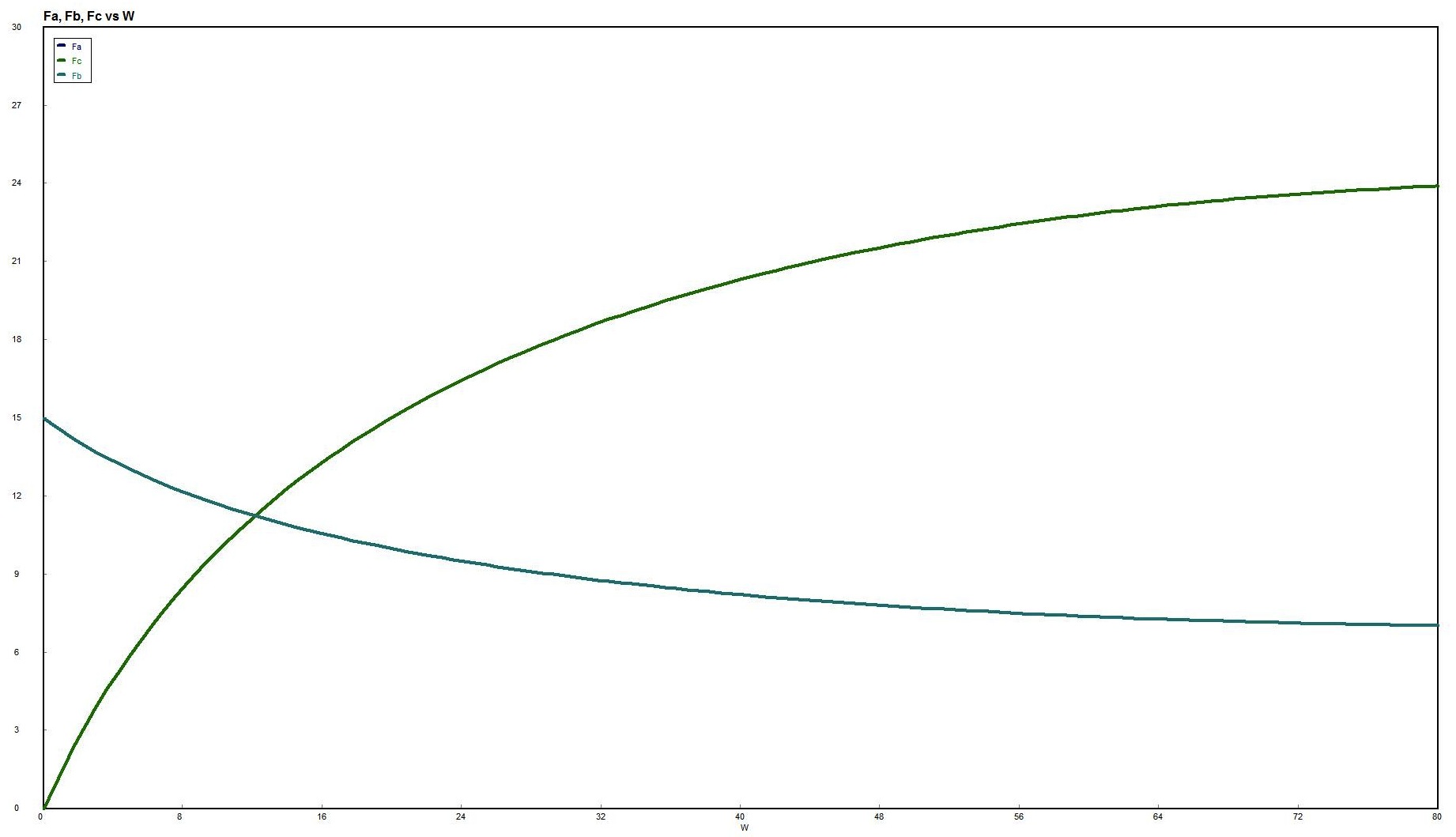
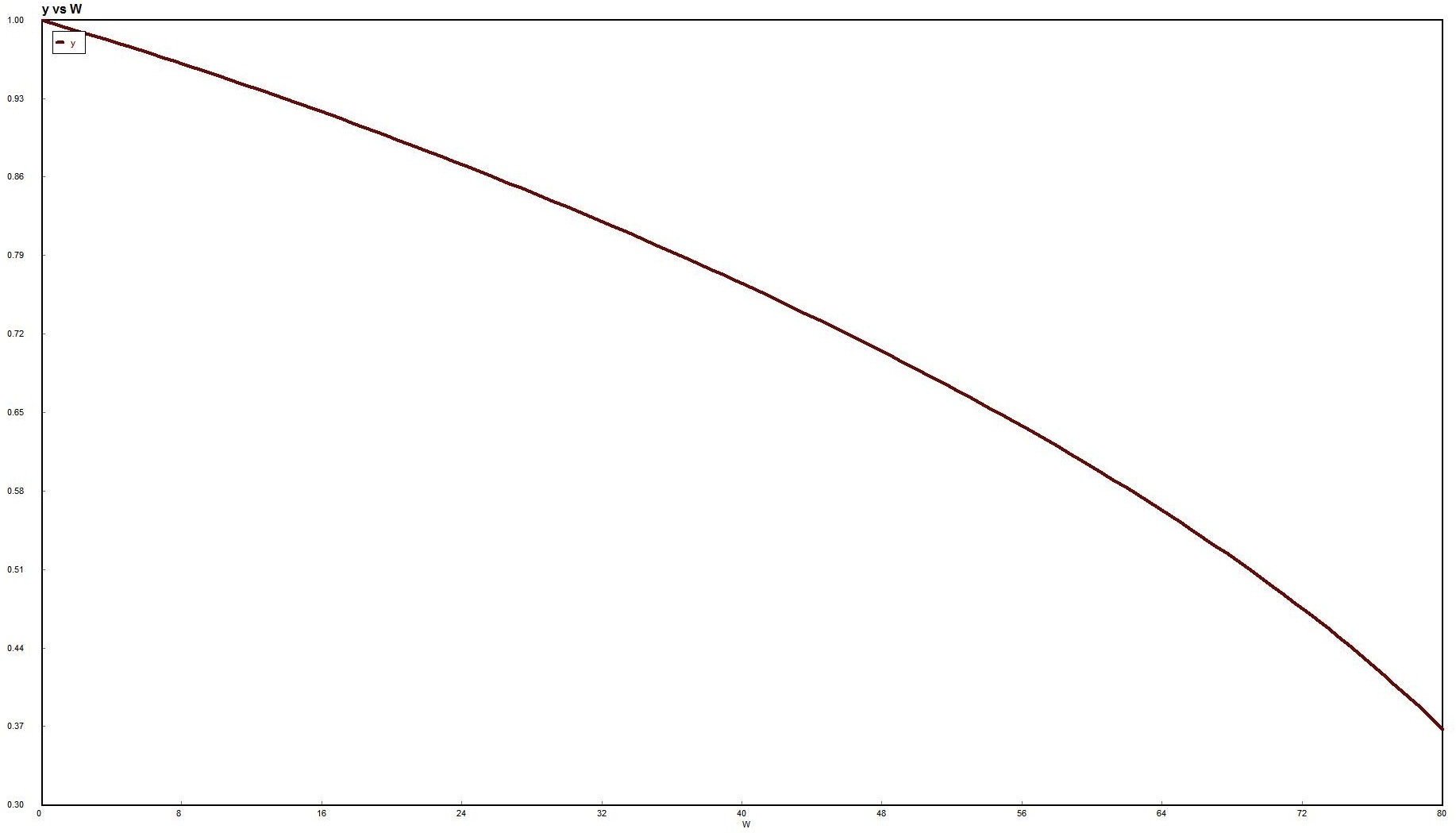
The following is an example problem from the book. It is located on page 235 in Chapter 6. This is a problem done in polymath and the .pol file has been included for reference. The report and accompanying graphs generated in Polymath are also shown.

Note that Differential equations 4 is changed to : $ d(p)/d(W) = -(\textrm{alpha} / (2 * p)) * (Ft / Ft0) $

B. Chapter 6 Semibatch ODE Solver Algorithm

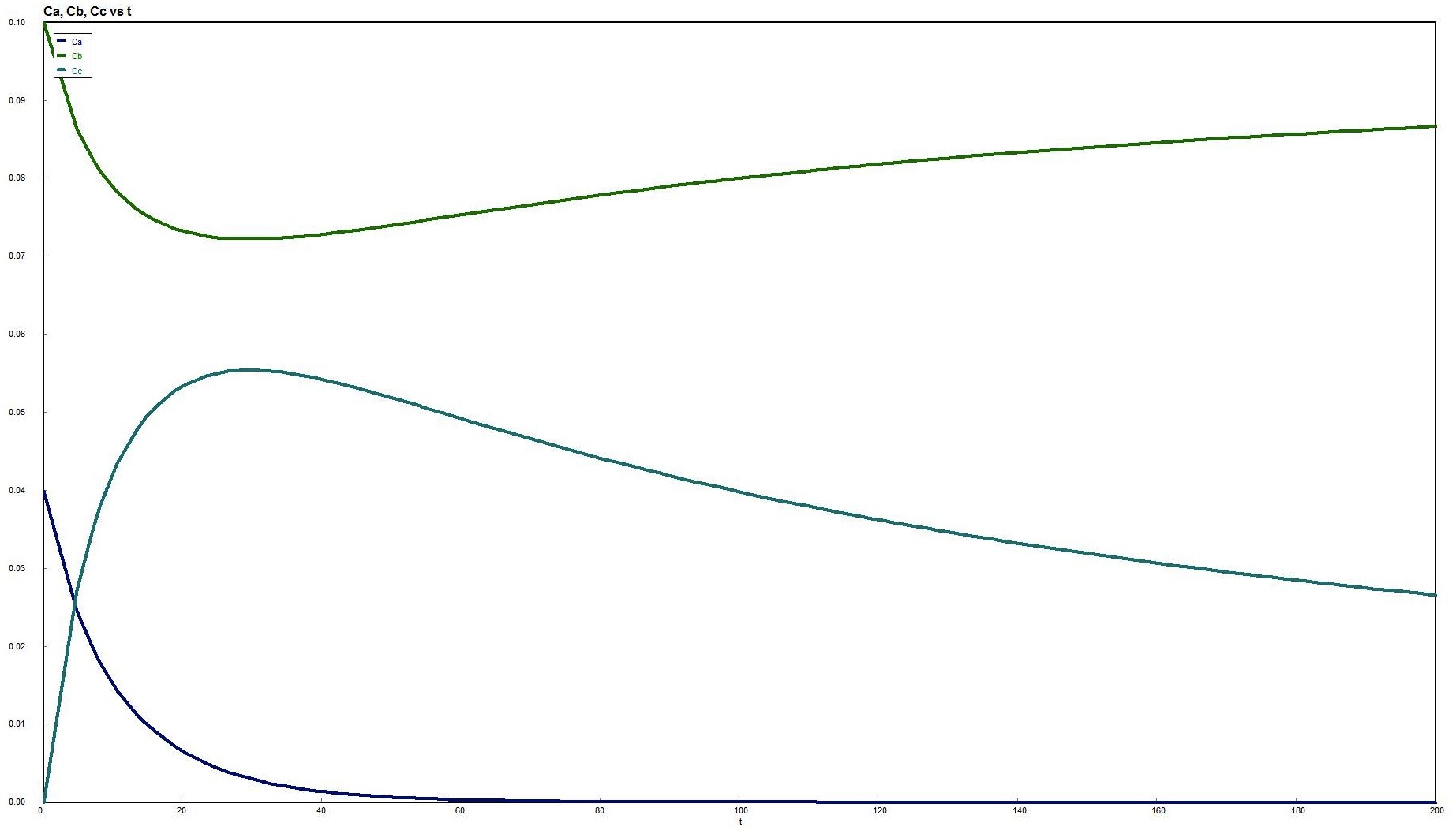
This is the second polymath problem from this chapter, shown on page 235 as well. The polymath file is included again, along with similar images.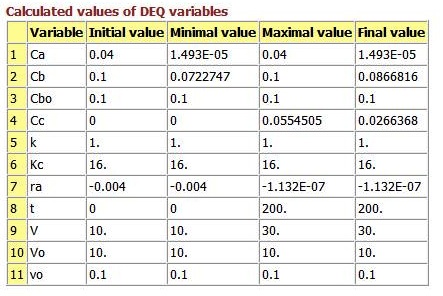

 

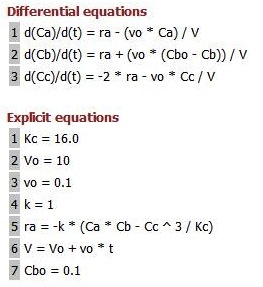
^* All chapter references are for the 1st Edition of the text Essentials of Chemical Reaction Engineering .

top