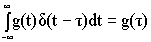| Select Chapter >> | TOC | Preface | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Appendices |
Chapter 16: Distributions of Residence Times for Chemical Reactors
Topics
| Residence Time Distribution | top |
We shall use the RTD to characterize existing (i.e. real) reactors and then use it to predict exit conversions and concentrations when reactions occur in these reactors.
Inject a tracer and measure exit concentration, CT(t).
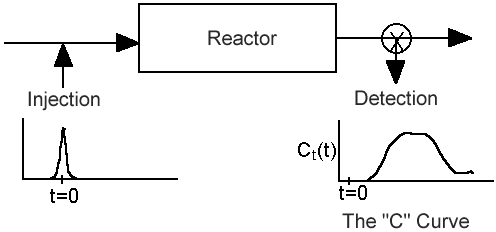
From the exit tracer concentration we can determine the following information:
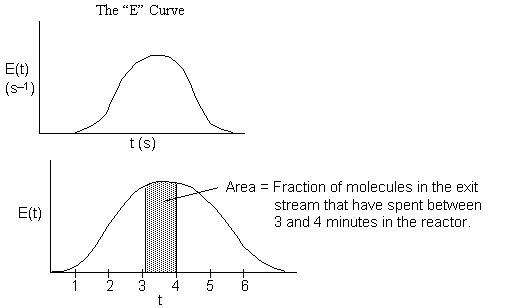
A. RTD (Residence Time Distribution) Function (E(t))
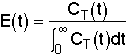
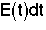= Fraction of molecules exiting the reactor that have spent a time between (t) and
(t + dt) in the reactor.
B. The Cumulative Distribution Function F(t)
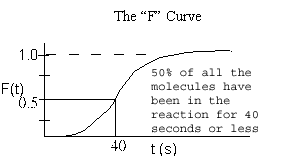
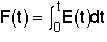= Fraction of molecules exiting the reactor that have spent a time t or less in the reactor.
= Fraction of molecules that have spent a time t or greater in the reactor.
C. Definitions
1. Mean Residence Time
Residence Time Distribution Analysis using COMSOL Multiphysics
2. Variance
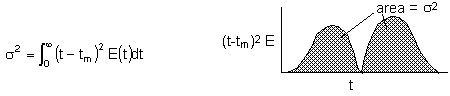
3. Space Time - For no dispersion/diffusion and v = v0, the space time equals the mean residence time.
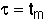
4. Internal Age Distribution,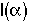
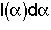= Fraction of molecules inside the reactor that have been inside the reactor between a time
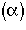and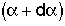
.
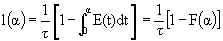
5. Life Expectancy
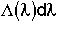= Fraction of molecules inside the reactor with age
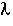that are expected to leave the reactor in a time
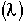to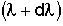
.
From our experimental data of the exit tracer concentration from pulse trace test
|
t(min) |
: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
C(mg/m3) |
: |
0 |
0 |
0.1 |
0.2 |
0.3 |
0.1 |
0 |
We can obtain
->
-> 
-> 
->
Calculate E(t), t and s2
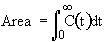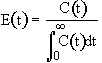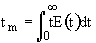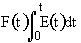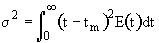
| RTD for Ideal Reactors | top |
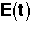 for Ideal Reactors
|
||
| PFR- Inject a pulse at t=0 |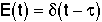 
|
|
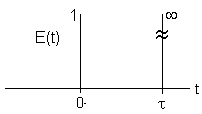
Dirac Delta Function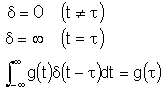
|
||
| CSTR | 
|
|
|
| Laminar (LFR) |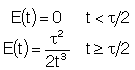 
|
|
|
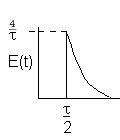
| RTD to Diagnose Faulty Operation | top |
Experimentally injecting and measureing the tracer in a laminar flow reactor can be a difficult task, if not a nightmare. For example, if one uses tracer chemicals that are photo-activated as they enter the reactor, the analysis and interpretation of E(t) from the data becomes much more involved.
Diagnostics and Troubleshooting
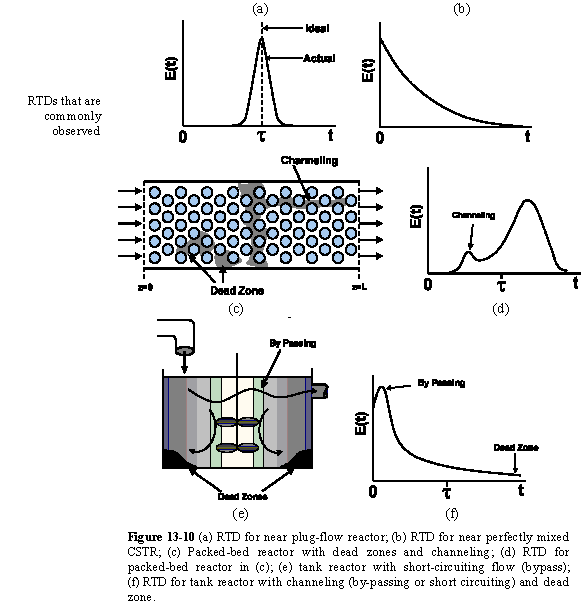
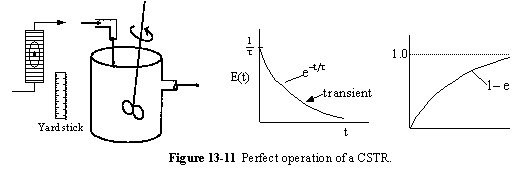
The CSTR
| Concentration |  |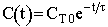
||
| RTD Function |  |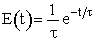
||
| Cumulative Function |  |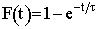
||
| Space Time |  |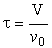
a. Perfect Operation
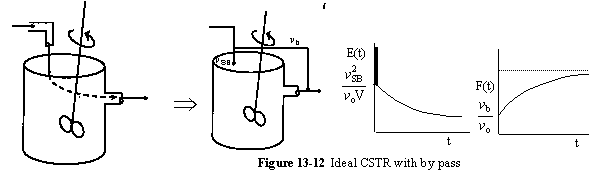
b. Passing (BP)
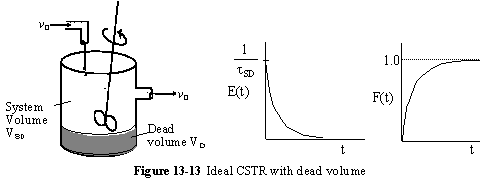
c. Dead Volume
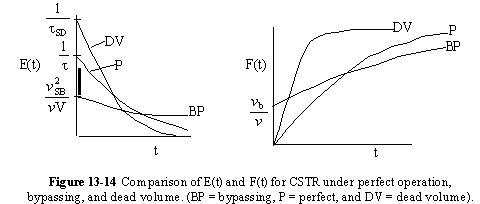
A summary for ideal CSTR mixing volume is shown in Figure 13-14
Tubular Reactor
A similar analysis to that for a CSTR can be carried out on a tubular reactor.
a. Perfect Operation of PFR (P)
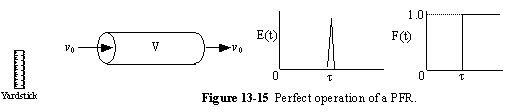
b. PFR with Channeling (Bypassing, BP)
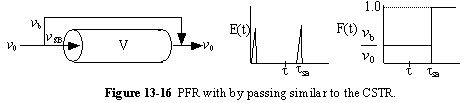
c. PFR with Dead Volume (DV)
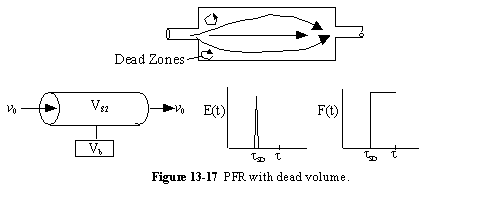
A summary for PRF is shown in Figure 13-18
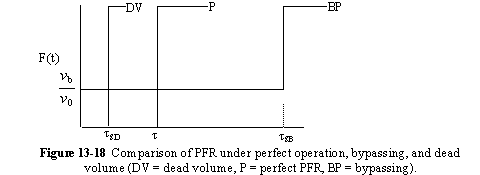
In addition to its use in diagnosis, the RTD can be used to predict conversion in existing reactors when a new reaction is tried in an old reactor. However, the RTD is not unique for a given system, and we need to develop models for the RTD to predict conversion.
Mean Residence Time
Using the E(t) curves
Drawing the F(theta) curves for the above ideal reactors
Matching Reactors with Tracer Step Inputs
Matching Reactor Models with E(t)
Medicinal Uses of RTD
Object Assessment of Chapter 16 * All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .