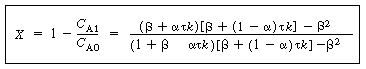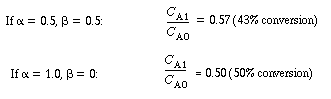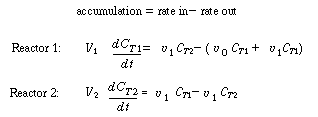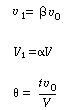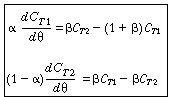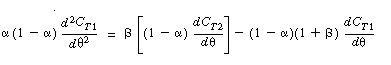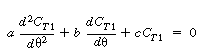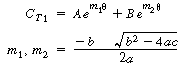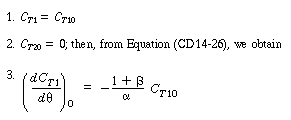Chapter 18: Models for Nonideal Reactors
Professional Reference Shelf
R18.2: Real Reactor Modeled as an Ideal CSTR with an Exchange Volume
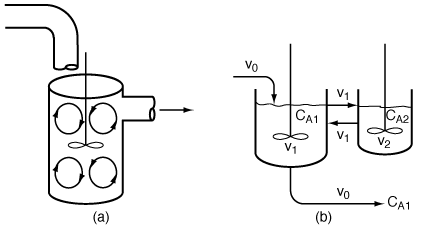
| In this particular model there is a highly agitated region in the vicinity of the impeller; outside this region, there is a region with less agitation (Figure R14.2-1). There is considerable material transfer between the two regions. Both inlet and outlet flow channels connect to the highly agitated region. We shall model the highly agitated region as one CSTR, the quieter region as another CSTR, with material transfer between the two. The material balances describing the steady-state behavior of the two reactors are | |||
|
(a) Real reaction systems; (b) model reaction system |
|||
Mole balances |
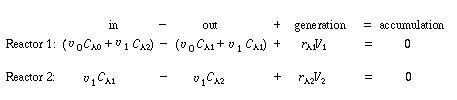 |
(R14.2-1) (R14.2-2) |
|
The two parameters in this model are the exchange flow rate 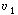 and
the volume of the highly agitated region, V1. Note that the measured volume
V is just the sum of V1
and V2. and
the volume of the highly agitated region, V1. Note that the measured volume
V is just the sum of V1
and V2. |
|||
| These two simultaneous algebraic equations can readily be solved for most rate laws. We shall first consider the case of a first-order reaction: | |||
|
|
(R14.2-3) | ||
Let 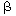 represent that fraction of the total flow that is exchanged
between reactors 1 and 2: represent that fraction of the total flow that is exchanged
between reactors 1 and 2: |
|||
|
|
(R14.2-4) | ||
and let 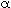 represent that fraction of the total
volume V occupied by the highly represent that fraction of the total
volume V occupied by the highly |
|||
| agitated region: | |||
|
Two parameters: |
|
(R14.2-5) | |
| Then | |||
|
|
(R14.2-6) | ||
| The space-time is | |||
|
|
|||
| With these specifications the balance on reactor 2 becomes | |||
|
|
(R14.2-7) | ||
| Solving for C A2 gives us | |||
|
|
(R14.2-8) | ||
| Substituting this value for C A2 into the mole balance on reactor 1, Equation (R14.1-1) yields | |||
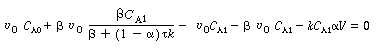 |
(R14.2-9) | ||
| Solving for C A1 we have | |||
|
|
(R14.2-10) | ||
| In terms of conversion, | |||
|
Conversion for the |
|
(R14.2-11) | |
For large values of the product 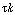 , , |
|||
|
(R14.2-12) | ||
we observe that the exit concentration is a function of the relative
sizes of the reactor volumes but not of the fluid exchanged between the two volumes.
This statement will also be true for the case where.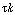 , , |
|||
|
|
(R14.2-13) | ||
|
Limiting situations |
which shows the consistency of our equation. If |
||
|
|
|||
We shall soon show how the two parameters 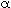 and and 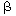 may be determined from tracer tests.
may be determined from tracer tests. |
|||
Determination of the Parameters 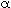 and and
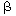 . .In more complex models, unfortunately, the determination of the parameters in the model is not straightforward, and they usually must be calculated by nonlinear regression using the predicted tracer response curve directly. Exceptions do exist to this general rule, though: Consider, for example, the two-CSTRs-with-interchange model described earlier (shown in Figure R14.2-2 in simplified form). A mole balance on a tracer pulse injected at t = 0 for each of the tanks is |
|||
|
Unsteady-state balance of inert tracer |
|
||
|
Model system |
|
||
| C T1 and C T2 are the tracer concentrations in reactors 1 and 2, respectively, with C T10 =N T 0 /V 1 and C T20 = 0. As before, | |||
|
|
(R14.2-4) (R14.2-5) |
||
| Substituting, we arrive at two coupled differential equations describing the unsteady behavior of the tracer that must be solved simultaneously. | |||
|
|
(R14.2-14) (R14.2-15) |
||
To obtain a solution, we first differentiate Equation (R14.2-14) with
respect to u and then multiply through by (1 - 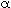 )
to get )
to get |
|||
|
(R14.2-16) | ||
| Substituting Equation (R14.2-15) for the bracketed term on the right-hand side gives us | |||
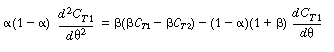
|
(R14.2-17) | ||
| The term C T2
in Equation (R14.2-17) is eliminated by solving Equation (R14.2-14) for |
|||
|
Solution technique commonly encountered in reactor modeling |
|
(R14.2-18) | |
| Combining Equations (R14.2-17) and (R14.2-18) and rearranging, we get |
|||
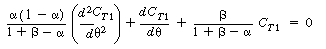 |
(R14.2-19) | ||
| which is of the form | |||
|
|
|||
| the solution to which is | |||
|
|
|||
| For the problem at hand, the initial conditions at |
|||
|
|
|||
| The corresponding solution for the tracer outlet concentration is | |||
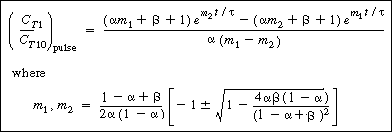
|
(R14.2-20) | ||
|
Plot in CT1as a function of time find
|
When tank 1 is rather small in comparison with tank 2 (small 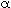 ), and the rates of transfer between the two reactors
are small (small ), and the rates of transfer between the two reactors
are small (small 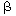 ), then during the first portion of the response to
a pulse input the second exponential term approximates to 1. During the second portion
of the response, the first exponential term approximates to zero. If the logarithm
of the tracer concentration is plotted as a function of time, the response curve
will approach a straight line at the two ends of the curve, and the parameters may
be obtained from the slopes and intercepts of these lines. This concept has been
used in physiological systems. 2 ), then during the first portion of the response to
a pulse input the second exponential term approximates to 1. During the second portion
of the response, the first exponential term approximates to zero. If the logarithm
of the tracer concentration is plotted as a function of time, the response curve
will approach a straight line at the two ends of the curve, and the parameters may
be obtained from the slopes and intercepts of these lines. This concept has been
used in physiological systems. 2 |
||