| Energy Balances, Rationale and Overview | top |
Nitrogen triiodide is unstable, and reacts exothermically when agitated.
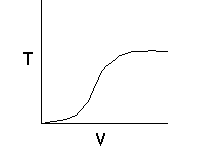
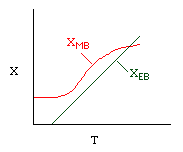
Let's calculate the volume necessary to achieve a conversion, X, in a PFR for a first-order, exothermic reaction carried out adiabatically. For an adiabatic, exothermic reaction the temperature profile might look something like this:



The combined mole balance, rate law, and stoichiometry yield:
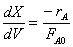 |
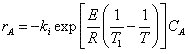 |
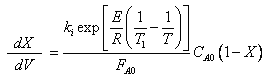 |
To solve this equation we need to relate X and T.
We will use the Energy Balance to relate X and T. For example, for an adiabatic reaction, e.g.,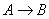 , in which no inerts the energy balance yields
, in which no inerts the energy balance yields
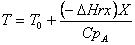
We can now form a table like we did in Chapter 2,

| User Friendly Energy Balance Equations | top |
The user friendly forms of the energy balance we will focus on are outlined in the following table.
User friendly equations relating X and T, and Fi and T 1. Adiabatic CSTR, PFR, Batch, PBR achieve this:
2. CSTR with heat exchanger, UA(Ta-T) and large coolant flow rate.
3A. In terms of conversion, X
3B. In terms of molar flow rates, Fi
4. For Multiple Reactions
5. Coolant Balance
|
||||||||||||||
These equations are derived in the text. These are the equations that we will use to solve reaction engineering problems with heat effects. |
| Energy Balance | top |
In the material that follows, we will derive the above equations.
We need to put the above equation into a form that we can easily use to relate X and T in order to size reactors. To achieve this goal, we write the molar flow rates in terms of conversion and the enthalpies as a function of temperature. We now will "dissect" both Fi and Hi. [Note: For an animated derivation of the following equations, see the Interactive Computer Modules (ICMs) Heat Effects 1 and Heat Effects 2.]
Flow Rates, Fi |
||
For the generalized reaction:
|
|
|
In general,
|
||
Assuming no phase change: |
||
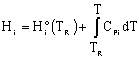 |
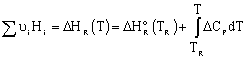 |
|
|
||
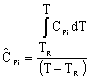 |
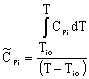 |
|
|
||
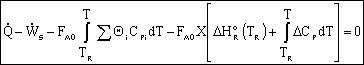 |
||
|
||
Adiabatic Energy Balance: |
|
 | |
Adiabatic Energy Balance for variable heat capacities: |
|
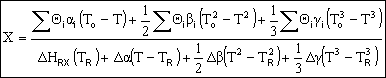
For constant heat capacities:
We will only be considering constant heat capacities for now. | |
| Reversible Reactions | top |
Consider the reversible gas phase elementary reaction.
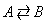
The rate law for this gas phase reaction will follow an elementary rate law.
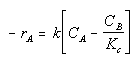
Where Kc is the concentration equilibrium constant. We know from Le Chaltlier's Law that if the reaction is exothermic, Kc will decrease as the temperature is increased and the reaction will be shifted back to the left. If the reaction is endothermic and the temperature is increased, Kcwill increase and the reaction will shift to the right.
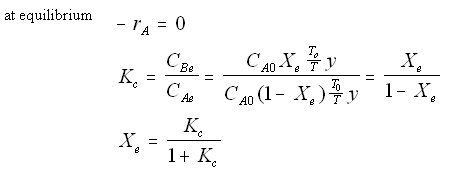
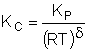
|
Van't Hoff Equation
|
For the special case of Integrating the Van't Hoff Equation gives: |
|
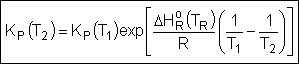
|
|
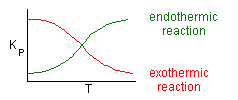
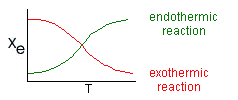
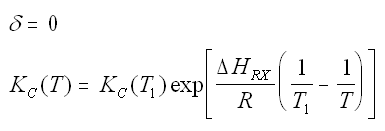
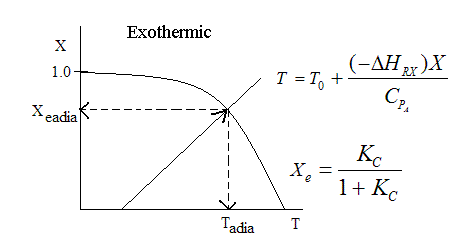
Adiabatic Equilibrium
Conversion on Temperature
Exothermic ΔH is negative
Adiabatic Equilibrium temperature (Tadia) and conversion (Xeadia
Endothermic ΔH is positive
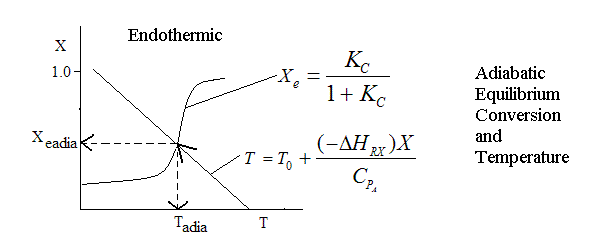
| Adiabatic Reactions | top |
Algorithm Adiabatic Reactions:
Suppose we have the Gas Phase Reaction
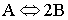
that follows an elementary rate law. To generate a Levenspiel plot to size CSTRs and PFRs we use the following steps or as we will see later use POLYMATH.
| 1. Choose X | |
| Calculate T | 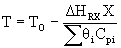
|
| Calculate k | 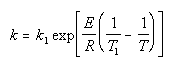
|
| Calculate KC | 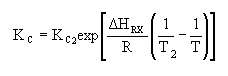
|
| Calculate To/T | |
| Calculate CA | 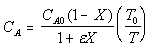
|
| Calculate CB | 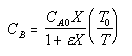
|
| Calculate -rA | 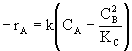
|
| 2. Increment X and then repeat calculations. | |
| 3. When finished, plot |
|
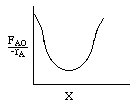 Levenspiel Plot for an exothermic, adiabatic reaction. We can now use the techniques developed in Chapter 2 to size reactors and reactors in series to compare and size CSTRs and PFRs. |
|
Consider: 
|
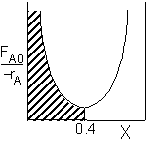
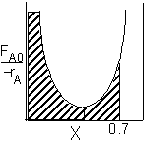
|
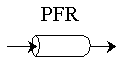 PFR Shaded area is the volume. PFR Shaded area is the volume. |
||
For an exit conversion of 40% |
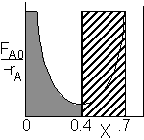
For an exit conversion of 70% |
|
|
|
|
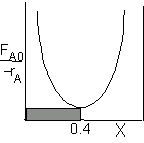
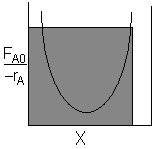
| CSTR |
||
For an exit conversion of 40% |
For an exit conversion of 70% |
|
|
|
|
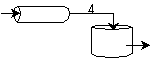
We see for 40% conversion very little volume is required. CSTR+PFR |
||
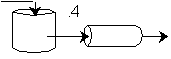
|
|
|
| (a) | (b) | |
For an intermediate conversion of 40% and exit conversion of 70% |
||
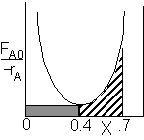
|
|
|
| (a) | (b) | |
Looks like the best arrangement is a CSTR with a 40% conversion followed by a PFR up to 70% conversion.
| Applications of the PFR/PBR User Friendly Energy Balance Equations | top |
NOTE: The PFR and PBR formulas are very similar.
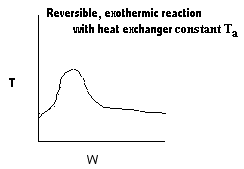 |
 |
|
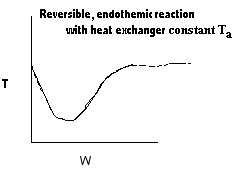
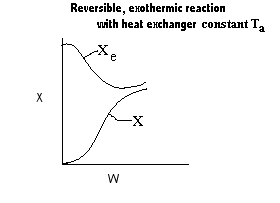 |
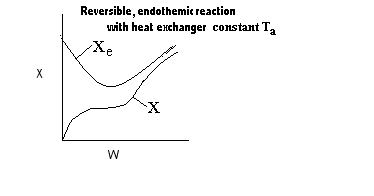 |
|
If we include pressure drop: |
||
C. |
||
Note: the pressure drop will be greater for exothermic adiabatic reactions than it will be for isothermal reactions |
||
 |
||
Balance on Heat Exchanger Coolant Solve simultaneously using an ODE solver (Polymath/MatLab). If Ta is not constant, then we must add an additional energy balance on the coolant fluid: |
||
| Co-Current Flow | 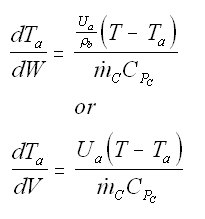 | |
| Counter-Current Flow |
with Ta = Tao at W = 0 |
|
For an exothermic reaction: with counter current heat exchange
|
|
A Trial and Error procedure for counter current flow problems is required to find exit conversion and temperature.
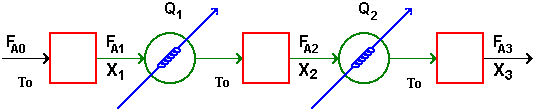
| Interstage Cooling/Heating | top |
|
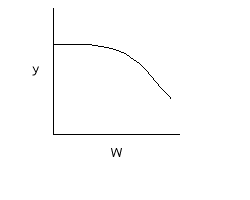
Curve A: Reaction rate slow, conversion dictated by rate of reaction and reactor volume. As temperature increases rate increases and therefore conversion increases. |
||
Interstage Cooling: |
||
|
||

|
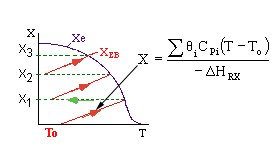
|

|
1.) |
Given X |
|
2.) |
Given T |
|
3.) |
Given V |
|
 |
||
| Evaluating the Heat Exchanger Term | top |
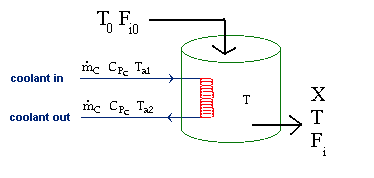
|
|
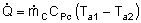
|
|
Assuming the temperature inside the CSTR, T,
is spatially uniform: |
|
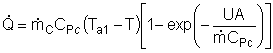
|
|
At high coolant flow rates the exponential term will be small, so we can expand the exponential term as a Taylor Series, where the terms of second order or greater are neglected, then: |
|
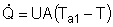
|
|
|
|
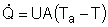
|
|
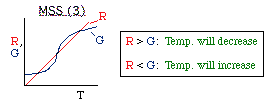
| Multiple Steady States (MSS) | top |
| From pagem 593 we can obtain | |
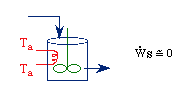 |
|
where |
|
 |
|
 |
Now we need to find X. We do this by combining the mole balance, rate law, Arrhenius Equation, and stoichiometry.
For the first-order, irreversible reaction A --> B, we have:
|
||
where |
||
At steady state: |
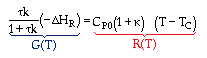 |
|
Substituting for k... |
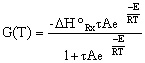
|
|
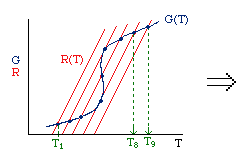 |
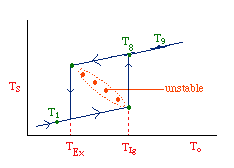 |
|
| Multiple Reactions with Heat Effects | top |
To account for heat effects in multiple reactions, we simply replace the term (-delta HRX) (-rA) in equations (8-60) PFR/PBR and (8-62) CSTR by:
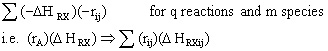
These equations are coupled with the mole balances and rate law equations discussed in Chapter 6.
Example: Consider the following gas phase reactions
|
|

We now substitute the various parameter values (e.g. delta HRX, E, U) into equations (1)-(13) and solve simultaneously using Polymath.
Hint for P8-15: G(T) = X(-ΔH°RX). Next Solve for X as a fuction of Γ CS0, μ1max, Cs = CS0(1-X), etc.
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .