next up previous contents
Next: Feladat: trapéz módszer Up: Gáz és plazma dinamika Previous: Feladat: implicit idõintegrálás kontinuitási   Tartalomjegyzék


Konzisztencia és a diszkretizáció rendje

Az elõzõ fejezetekben tárgyalt módszerek különbözõ stabilitási tulajdonságokat mutattak. Az FTCS módszer feltétel nélkül instabil, az upwind módszer feltételesen stabil, az implicit idõintegrálással kombinált centrális differencia módszer feltétel nélkül stabil a kontinuitási egyenlet megoldására. Ugyanakkor a stabil upwind és az implicit centrális differencia módszerek által adott megoldások rendkívül pontatlanok voltak. Ebben a fejezetben megpróbáljuk javítani a megoldás pontosságát.

A (10) által definiált upwind módszer hibáját a következõképpen becsülhetjük meg. Fejtsük Taylor sorba a folytonosnak és többszörösen deriválhatónak feltételezett megoldást az $x_j, t_n$ téridõ pont körül:

$\displaystyle \rho(x,t)= \rho_j^n$ $\textstyle +$ $\displaystyle (x-x_j)\partial_x\rho + \frac12(x-x_j)^2\partial_{xx}\rho$ (18)
  $\textstyle +$ $\displaystyle (t-t_n)\partial_t\rho + \frac12(t-t_n)^2\partial_{tt}\rho + (x-x_j)(t-t_n)\partial_{xt}\rho + \ldots$  

Fejezzük ki a (10)-ben szereplõ diszkrét értékeket a sorfejtés alapján másodrendig elmenve
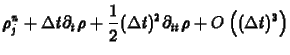$\displaystyle \rho_j^{n+1}$ $\textstyle =$ $\displaystyle \rho_j^n + \Delta t \partial_t \rho + \frac12 (\Delta t)^2 \partial_{tt} \rho + O\left((\Delta t) ^3\right)$ (19)
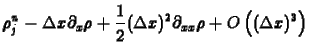$\displaystyle \rho_{j-1}^n$ $\textstyle =$ $\displaystyle \rho_j^n - \Delta x \partial_x \rho + \frac12 (\Delta x)^2 \partial_{xx} \rho + O\left((\Delta x) ^3\right)$ (20)

Helyettesítsük be a fenti sorfejtéseket az upwind módszer (10) formulájába, és egyszerûsítsünk:
\begin{displaymath} \partial_t \rho + \frac12 \Delta t \partial_{tt} \rho + O(\... ...x\rho + v \frac12 \Delta x \partial_{xx}\rho + O(\Delta x^2) \end{displaymath} (21)

Mint látható, vezetõ rendben $\partial_t \rho = -v\partial_x\rho$, azaz a (3) egy dimenziós kontinuitási egyenletet kaptuk vissza konstans sebességgel. Ez azt jelenti, hogy a diszkretizáció konzisztens az analitikus PDE-vel. Magasabb rendben azonban fellépnek $\Delta x$-szel és $\Delta t$-vel arányos további tagok is, melyek a diszkretizációs hibát okozzák. Jelen esetben a hiba tagok lineárisan arányosak a rácstávolsággal és az idõlépéssel, ezért az upwind módszer térben és idõben elsõrendû.

Könnyen megmutatható, hogy a centrális differencia módszer térben másodrendben pontos. Az explicit FTCS módszer azonban instabil. A (16) egyenletben felírt teljesen implicit centrális differencia módszer rendkívül diffúzív. Ennek az az oka, hogy az idõderivált hibája ugyanúgy elsõrendû, mint az upwind módszernél. Ezen javít a trapéz módszer, melyben a térbeli deriváltat az $n$-dik és $n+1$-dik lépések átlagával közelítjük. A kontinutási egyenlet esetében az idõben trapéz térben centrális differencia módszer, más néven a Crank-Nicholson módszer, a

\begin{displaymath} \frac{\rho_j^{n+1}-\rho_j^n}{\Delta t}+ \frac12\left[v\fr... ...\frac{\rho^{n+1}_{j+1}-\rho^{n+1}_{j-1}}{2\Delta x} \right]=0 \end{displaymath} (22)

formában írható. Annak ellenére, hogy ez a módszer térben és idõben másodrendû, meglehetõsen pontatlan eredményt ad a kontinuitási egyenlet megoldásánál még kis idõlépések esetén is. Ennek okát a komplex $G$ erõsítési faktor alapján lehet megérteni. A (22) egyenlet stabilitás vizsgálatából
\begin{displaymath} G=\frac{1-i (C/2) \sin(k\Delta x)}{1+i (C/2) \sin(k\Delta x)} \end{displaymath} (23)

Könnyen látható, hogy $\vert G\vert=1$, azaz a trapéz módszer feltétel nélkül stabil, sõt a Fourier komponensek amplitúdója pontosan megmarad. Ugyanakkor a fázis sebesség, ami $G$ komplex fázisszögével áll kapcsolatban, rendkívül erõsen függ a hullámhossztól.

Egy implicit idõlépés jóval több számítást igényel mint egy explicit idõlépés az egyenletrendszer megoldása miatt, ez a különbség különösen több dimenziós problémáknál válik jelentõssé. Szerencsére számos feltételesen stabil és másodrendben pontos explicit módszer létezik. Ezek közül az egyik legegyszerûbb és legnépszerûbb a MacCormack módszer, mely két lépésbõl áll. Az elsõ lépésben egy bal oldali térbeli deriváltat alkalmazunk, a másodikban pedig egy jobb oldalit, majd a két eredményt átlagoljuk. Továbbá, a második lépésben már az elsõ lépés eredményét használjuk, ami idõben másodrendû pontossághoz vezet. A kontinuitási egyenletre a MacCormack módszer a következõképpen írható fel:

$\displaystyle \rho_j^*$ $\textstyle =$ $\displaystyle \rho_j^n-v\Delta t \frac{\rho_j^n-\rho_{j-1}^n}{\Delta x}$ (24)
$\displaystyle \rho_j^{**}$ $\textstyle =$ $\displaystyle \rho_j^n-v\Delta t \frac{\rho_{j+1}^*-\rho_j^*}{\Delta x}$ (25)
$\displaystyle \rho_j^{n+1}$ $\textstyle =$ $\displaystyle \frac{\rho_j^*+\rho_j^{**}}{2}$ (26)


Alfejezetek
next up previous contents
Next: Feladat: trapéz módszer Up: Gáz és plazma dinamika Previous: Feladat: implicit idõintegrálás kontinuitási   Tartalomjegyzék
Gabor Toth 2000-09-04