All electrostatic applications derive their capabilities from Coulomb's Law. Under this relation, the force between the two charged particles is proportional to both of the individual charges (say, q1 and q2) and inversely proportional to the square of the distance separating the charges (r). The exact form is given by

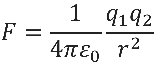
where, ke,

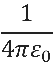
is the constant of proportionality [Crowley]. The constant ε0 is called the permittivity of free space, and its value is 8.85410-12 F/m. A positive force value (either two positive or two negative charges interacting) results in a repulsive force, while a negative force term from the interaction of two oppositely charged particles is attractive.

    Of course, the idea of point charges described by q1 and q2 are idealized. However, even though this idealized concept doesn't exist, we can approximate charged spheres as point charges. For more complicated shapes, we can use the equation,

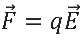
where E is the electric field and q is the charge of the object the force is acting on (Griffiths 60).

    This equation (along with Coulomb's Law in multiple dimensions) obeys the superposition principle, which allows us to model a complicated system of overlapping electric fields by simply finding the vector sum of each individual field. The electric field of a point charge is

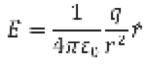
where r is a unit vector pointing away from the point charge. As the reader can see, if we plug this electric field back into Eq. 2, we return to our original relation, Coulomb's Law (Eq. 1).

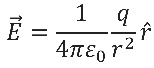
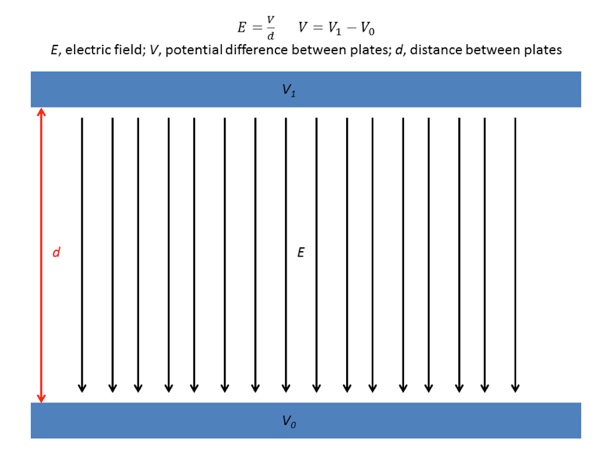
    In our case, we are looking at the evolution of paint particles after they have been electrically charged and sprayed onto a surface. We assume the paint has not dried yet, so together the particles behave as a film, under the influence of surface tension and the strength of the applied electrostatic field (that deposited them onto the substrate's surface). We neglect the particle's mutual repulsion of each other, because this would produce a tensile force spreading out the film, similar to surface tension. We model a uniform electric field between a parallel plate capacitor (shown in the figure below), where a hole in the top plate spews the electrically charged paint droplets onto the oppositely charged substrate. The parallel plate capacitor model was an obvious choice because it would result in uniform paint distribution.

The electric field produced by the parallel plate capacitor is given by (Eq. 4),

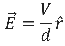
where V is the potential difference between the charged plates, d is the distance separating the plates, and  is the direction pointing towards the lower potential. We also generalize point charges to line charges, where  (Eq. 5); 

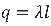
is the charge per unit length and l is the length of the charged segment (in 2-D). We combine Eqs. 4 and 5 to determine our force applied to each segment:  (Eq. 6).

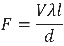
To simplify the FEM code, we applied

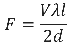
at end node of the element.