|
|
Optimal Graph Crossmath Model for Kidney Paired Donation (KPD) Program [Software Demo]
|
Problem
Definition
-
Kidney transplantation has emerged as the treatment for
the most serious forms of kidney disease. However, there is
a considerable shortage of donor kidneys in the U.S.: more
than 80;000 patients are on the waiting list for transplants
by the end of 2010. In the real world clinical application,
deceased donation and living donation are the two resources
of organs for kidney transplantation, and living-donor transplant
has a higher chance of success. Unfortunately, about
one-third of patients with willing live donors will be excluded
from kidney transplantation because of ABO blood
type mismatch or HLA incompatibility. Therefore, KPD program is established as
a promising clinical solution to overcome the shortage of
donors. The essential idea of such program is to exchange
living kidney donors between two willing but incompatible donor-recipient pairs. The fundamental question in the KPD
program is how to make an optimal decision of kidney
exchanges that benefit patients the best.
 |
Algorithms
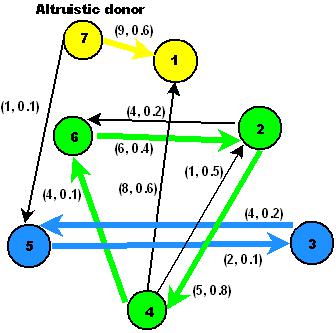
- A kidney exchange problem can be represented as a
directed graph G =(V, E). Let |V| be the number of vertices
(nodes) and |E| be the number of edges in a KPD graph,
where || denotes cardinality. Each vertex in graph G represents an incompatible donorrecipient
pair (e.g., vertex 1) or an altruistic donor (e.g.,
vertex 7). Each edge from vertex i to vertex j indicates
that the donor kidney in vertex i is compatible with the
recipient in vertex j (e.g., 7 ->1). In this directed graph,
each edge is assigned a weight representing edge utility ui j
of the kidney transplant from the donor in vertex i to the
recipient in vertex j (e.g., u_{71} = 9). In addition, an edge
probability pi j is considered for each edge to reflect the
possibility of an actual successful kidney transplant from i to
j (e.g., p_{71} = 0.6). All the directed edges are established for
compatibility of ABO blood types and HLA sensitizations (see
above Figure).
- The goal of optimization for kidney exchange program
is to find a collection of mutually disjoint cycles or chains that attain the maximum overall expected utility of graph G.
This task of optimizing matches on graph G by the following
setup of integer programming:
Results
- We compared two allocation strategies
in terms of accumulated number of transplants, in the
settings where the KPD only involved donor-recipient pairs
(namely no ADs). The two strategies to be compared are (1)
Cycle-Without-AD-Base: a traditional method that does not
consider the expected utility in the optimization; (2) Cycle-
Without-AD: a new method that uses the expected utility
and accounts for the chance of failure in the optimization. The accumulated number of transplants obtained by the
two approaches with different arrival rates shown in the following figures. It implies that
the more pairs participate in the kidney exchanges program,
the higher likelihood of achieving matches in the KPD pool.
Moreover, the accumulated number of transplants gained by
the new approach (i.e., Cycle-Without-AD) is significantly
higher than the traditional method (i.e., Cycle-Without-ADBase)
in the magnitude of 2-4 folds.
- We integrated the ADs into the new allocation
strategy and investigated the role of ADs in the kidney
exchanges. In the following figures (a)-(c) display the accumulated
number of transplants obtained by two strategies: (1) Cycle-
Without-AD and (2) Cycle-With-AD, where the edge utility
is generated from a uniform distribution on interval from
[10,10] to [10,30] and the arrival rate is 10. In these
panels, based on the accumulated number of transplants
over 12 match runs, method Cycle-With-AD gives at least
10% more matches than the method without using ADs.
Moreover, we plotted the results for the case of arrival rate equal to 20 in
the following figures (d)-(f). Again, when more people enters, method
with ADs clearly performed better than the one without ADs.
As a result, using ADs in the kidney exchanges would help
clinicians to achieve more transplants.
- We also compared accumulated utility of these two methods
(1) Cycle-Without-AD and (2) Cycle-With-AD. From the following figures (a)-(c),
we noticed that the accumulated utility of the Cycle-With-
AD method enjoys a gain between 15% to 30% over the
Cycle-Without-AD method when the edge utility distribution
changes from [10,10] to [10,30] with arrival rate equal to 10. Likewise,
in the following figures (d)-(f) report the accumulated utility of method
using ADs is about at least 10% higher than that of the
method not using ADs with arrival rate equal to 20. Therefore, it is obvious
that on average the method without using ADs is consistently
outperformed by the method using ADs over all match
runs in terms of accumulated utilities.
- We developed a general KPD computerized platform
and graphic user interface (GUI) that allow to model,
visualize, and monitor the real world kidney exchange
program. The following is a flowchart of computerized platform for kidney exchanges.
Related Publications
- Yanhua Chen, Jack Kalbfleisch, Yijiang Li, Peter X.-K. Song, and Yan Zhou,
"Computerized Platform for Optimal Organ Allocations in Kidney Exchanges,"
Proceedings of the 2011 International Conference of Bioinformatics and Computational Biology (BIOCOMP),
Las Vegas, NV, USA, 2011 (acceptance rate = 21%).
- Yanhua Chen and Peter X.-K. Song, "Computerized Decision Support System for Kidney Paired Donation Program
", Proceedings of 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC),
Boston, MA, USA, 2011.
- Yanhua Chen, Yijiang Li, Jack D. Kalbfleisch, Yan Zhou, Alan Leichtman and Peter X.-K. Song,
"Graph-based Optimization Algorithm and Software on Kidney Exchanges",
IEEE Transactions on Biomedical Engineering (TBME), Vol. 59, No. 7, pp. 1985-1991, July 2012
|
|
| |