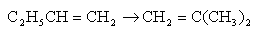Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 1: Mole Balances

Whenever the media player appears, audio is available for use, starting with the one below.
Sorry, your browser does not support the audio tag. Please try using a different browser or updating your current browser.

Topics

  1. Chemical Identity
  2. Reaction Rate
  3. General Mole Balance Equation
  4. Mole Balance on Different Reactor Types
  5. Self Test Exercises

Chemical Identity TOP

A chemical species is said to have reacted when it has lost its chemical identity. The identity of a chemical species is determined by the kind, number, and configuration of that species' atoms.

Reaction YouTube Video: Carbon Dioxide and Magnesium

Three ways a chemical species can lose its chemical identity:

1. decomposition
2. combination
3. isomerization
Reaction Rate top

Sorry, your browser does not support the audio tag. Please try using a different browser or updating your current browser.

The reaction rate is the rate at which a species looses its chemical identity per unit volume. The rate of a reaction can be expressed as the rate of disappearance of a reactant or as the rate of appearance of a product. Consider species A:

A → B

rA = the rate of formation of species A per unit volume
-rA = the rate of a disappearance of species A per unit volume
rB = the rate of formation of species B per unit volume

Example: A → B

If B is being created at a rate of 0.2 moles per decimeter cubed per second (i.e. the rate of formation of B is rB = 0.2 mole/dm3/s),
then A is disappearing at the same rate (-rA = 0.2 mole/dm3/s). This also means that the rate of formation of A is rA = -0.2 mole/dm3/s.

For a catalytic reaction, we refer to -rA', which is the rate of disappearance of species A on a per mass of catalyst basis.

NOTE: dCA/dt is not the rate of reaction

Is sodium hydroxide reacting?

Consider species j:

  • rj is the rate of formation of species j per unit volume [e.g. mol/dm3*s]
  • rj is a function of concentration, temperature, pressure, and the type of catalyst (if any)
  • rj is independent of the type of reaction system (batch, plug flow, etc.)
  • rj is an algebraic equation, not a differential equation

We use an algebraic equation to relate the rate of reaction, -rA, to the concentration of reacting species (e.g., CA) and to the temperature (T) at which the reaction occurs [e.g. -rA = k(T)CA2].

Sorry, your browser does not support the audio tag. Please try using a different browser or updating your current browser.

Would you like to see some other rates of reaction?
The Convention for Rates of Reaction

General Mole Balance Equation top

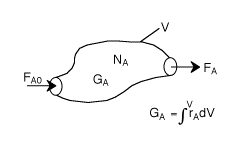
FA0= Entering molar flow rate of A (mol/time)
FA= Exiting molar flow rate of A (mol/time)
GA= Rate of generation(formation) of A (mol/time)
V = Volume (vol e.g. m3)
rA= rate of generation(formation) of A (mole/time•vol)
NA= number of moles of A inside the system Volume V (mol)
t = time (e.g. s)

How about testing what you've learned?

Mole Balance on Different Reactor Types top

The General Mole Balance Equation (GMBE) applied to the four major reactor types (and the general reaction, A → B):

Sorry, your browser does not support the audio tag. Please try using a different browser or updating your current browser.
Reactor Differential Algebraic Integral    
Batch  
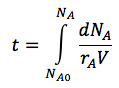CSTR      
PFR  
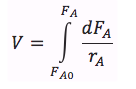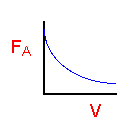PBR  

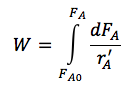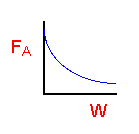Self Test Exercises top

Fourteen Multiple Choice Questions
Batch Reactor Time
What's Wrong With This Solution?
Smog in Los Angeles Basin Web Module
Getting Unstuck on a Problem and the Problem Solving Algorithm
Visual Encyclopedia of Chemical Reactors
 Polymath Tutorials
Objective Assessment of Chapter 1

The following humorous video is set to Randy Newman's song "You've got a friend in me" was made by Professor Lane's 2008 Chemical Reaction Engineering class at the University of Alabama, Tuscaloosa.

The following humorous video is set to Randy Newman's song "You've got a friend in me" was made by Professor Lane's 2008 Chemical Reaction Engineering class at the University of Alabama, Tuscaloosa. Reaction YouTube Video: Fogler Zone (You've Got a Friend in Fogler)

The following animation is an excerpt taken from the lecture slides that Professor Fogler uses in his Reactions course, illustrating the importance of "Keeping Up"

Keeping Up