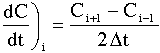Elements of
Chemical Reaction Engineering
6th Edition



Home

Essentials of
Chemical Reaction Engineering
Second Edition

  Select  Chapter  >>     TOC     Preface     1     2     3     4     5     6     7     8     9     10     11     12     13     14     15     16     17     18     Appendices  
›

By Chapter Hide

  • Objectives
  • Living Example Problems
  • Extra Help
  • - Summary Notes
  • - LearnChemE Screencasts
  • - FAQs
  • - Interactive Computer Modules
  • Additional Material
  • Self Test
  • i>Clicker Questions
  • Professional Reference Shelf

By Concept Hide

  • Interactive Modules
  • -Web Modules
  • -Interactive Computer Games
  • Living Example Problems

U of M Hide

  • Asynchronous Learning
  • ChE 344
  • ChE 528

Chapter 7: Collection and Analysis of Rate Data

Finding the Rate Law

Consider the following reaction that occurs in a constant volume batch reactor: (We will withdraw samples and record the concentration of A as a function of time.)

Mole Balance:

               

Rate Law:

Stoichiometry:

Combine:

Topics

  1. Integral Method
  2. Differential Method
  3. Non-Linear Least-Squares Analysis
Integral Method top

We could integrate the combined mole balance and rate law to plot reaction rate data in terms of concentration vs. time for 0, 1st, and 2nd order reactions.

Table 7.1- Derivation Equations used to Plot 0, 1st, and 2nd order reactions.

These types of plots are usually used to determine the values k for runs at various temperatures and then used to determine the activation energy.

                                      Table 7.1
Zero Order First Order Second Order

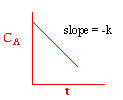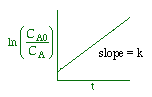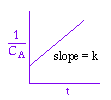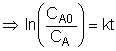If the data do not fall on a straight line for α=0,1, or 2 such as α=2;

then we should stop guessing reaction orders and proceed to either the differential method of analysis or to regression.

Differential Method top

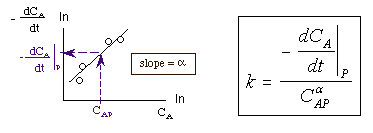
Taking the natural log of

The reaction order can be found from a ln-ln plot of:


Methods for finding the slope of log-log and semi-log graph papers may be found at http://www.physics.uoguelph.ca/tutorials/GLP/.

However, we are usually given concentration as a function of time from batch reactor experiments.

time (s) 0 t1 t2 t3
concentration (mol/dm3) CAo CA1 CA2 CA3

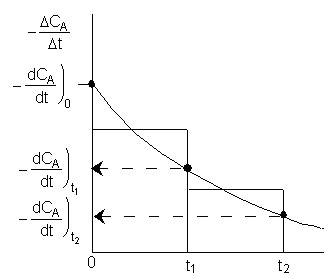
Three Ways to Determine (-dCA/dt) from Concentration-Time Data (Graphical,    Polynomial, Finite Difference, Non-Linear Least Squares Analysis)

2A. Graphical

       

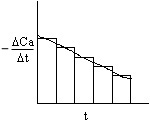
This method accentuates measurement error!

 

2B. Polynomial (using Polymath)

CA = ao + a1t + a2t2 + a3t3 +a4t4


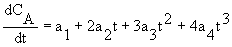
2C. Finite Difference

Non-Linear Least-Squares Analysis top

We want to find the parameter values (alpha, k, E) for which the sum of the squares of the differences, the measured parameter (Pm), and the calculated parameter (Pc) is a minimum.

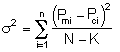
That is we want to be a minimum.

time (s) 0 t1 t2 t3
concentration (mol/dm3) CAo CA1 CA2 CA3



For concentration-time data, the measured parameter P has concentration CA. We can integrate the combined mole balance equation and rate law

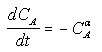
to obtain

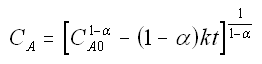
We now guess k and alpha and calculate each CACi at the times shown in the above table and then compare it with the measured concentration by taking the difference and squaring it.

We then sum up the differences for all the data points.



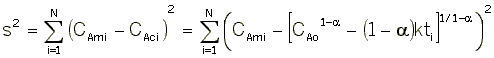
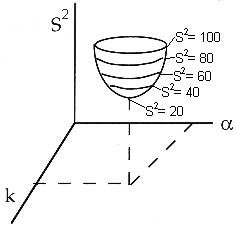
We continue to guess k and alpha until we find the values of alpha and k which minimize S2 (actually we let the computer find these values.)


"What is Wrong with This Solution?"
 Reactor Laboratory
 Polymath regression analysis tutorial
 Polymath non-linear regression analysis tutorial
 Polymath non-linear equation Solver Tutorial
 Excel non-linear regression analysis tutorial
 Object Assessment of Chapter 7

  * All chapter references are for the 1st Edition of the text Essentials of Chemical Reaction Engineering .

top