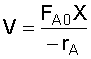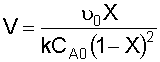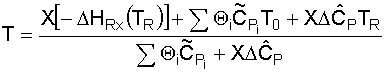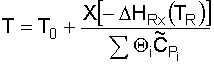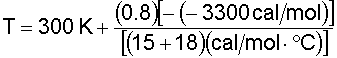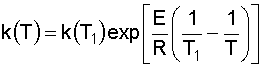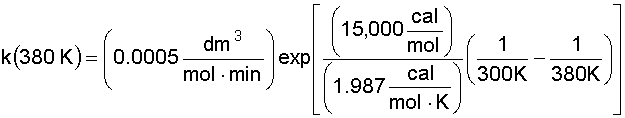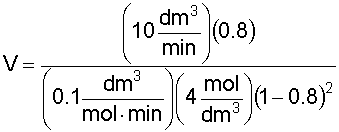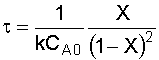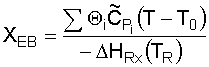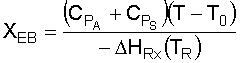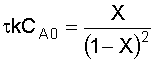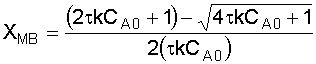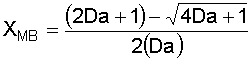Chapter 11: Nonisothermal Reactor Design: The Steady State Energy Balance and Adiabatic PFR Applications
Adiabatic Liquid Phase in A CSTR
Part BSecond Order Reaction Carried Out Adiabatically in a CSTR |
|||
|
(b) For part (b) we will again use the non isothermal
reactor design algorithm discussed in Chapter 8. The first four steps of
the algorithm we used in part (a) apply to our solution to part (b). It is
at step number 5, where the algorithm changes.
1. CSTR Design Equation:
2. Rate Law:
3. Stoichiometry: liquid,
4. Combine:
NOTE: We will find it more convenient to work with this equation in terms of space time, rather than volume: Given reactor volume (V), you must solve the energy balance and the mole balance
simultaneously for conversion (X), since it is a function of temperature (T).
5. Solve the Energy Balance for X EB as a function of T: From the adiabatic energy balance (as applied to CSTRs):
6. Solve the Mole Balance for X MB as a function of T: We'll rearrange our combined equation from step 4 to give us: Solving for X gives us: Let's simplify a little more, by introducing the Damköhler Number, Da:
We then have: 7. Plot X EB and X MB : You want to plot
X EB and
X MB on the same graph
(as functions of T) to see where they intersect. This will tell you where
your steady-state point is. To accomplish this, we will use Polymath (but
you could use a spreadsheet).
Plot of
X EB and
X MB versus T
We see that our conversion would be about 0.87, at a temperature of 387 K. |
Part CSecond Order Reaction Carried Out Adiabatically in a CSTR |
|||
|
(c) For part (c) we will simply modify the Polymath
program we used in part (b), setting our initial temperature to 280 K. All
other equations remain unchanged. 1. CSTR Design Equation:
2. Rate Law:
3. Stoichiometry: liquid,
4. Combine:
Given reactor volume (V), you must solve the energy balance and the mole balance
simultaneously for conversion (X), since it is a function of temperature (T). 5. Solve the Energy Balance for X EB as a function of T:
6. Solve the Mole Balance for X MB as a function of T: 7. Plot X EB and X MB : You want to plot
X EB and
X MB on the same graph
(as functions of T) to see where they intersect. This will tell you where
your steady-state point is. To accomplish this, we will use Polymath (but
you could use a spreadsheet). Plot of
X EB and
X MB versus T We see that our conversion would be about 0.75, at a temperature of 355 K. |