IOE 611
Nonlinear Programming


Instructor: Professor Katta G. Murty, 232 IOE Bldg., 763-3513, katta_murty@umich.edu
Prerequisites: A course in linear programming, equivalent
to IOE 510.
Course objectives: To expose the student to nonlinear
models, their applications, how to construct them, and to algorithms for solving them satisfactorily
Books:
- M.S. Bazaraa, H.D. Sherali, and C.M. Shetty, Nonlinear Programming Theory and Algorithms, Wiley, 1993, 2nd Edition.
- K.G. Murty, Linear Complementarity, Linear and Nonlinear
Programming, Helderman-Verlag, 1988.(This book is now available for
download).
- R. Fletcher, Practical Methods of Optimization, Wiley-Interscience, 1987.
Contents:
- Formulation of continuous optimization models, curve fitting, parameter estimation,
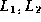 and
and 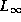 -measures of deviation.
Difference between linear and nonlinear model building. Examples.
-measures of deviation.
Difference between linear and nonlinear model building. Examples.
- Types of problems. State of the art. What can and cannot be done efficiently? Goals for algorithms.
- Theorems of alternatives for linear systems.
- Convex sets, separating hyperplanes, convex and concave functions.
- Optimality conditions.
- Quadratic programming and complementary pivot methods.
- Newton's method and simplicial methods for nonlinear equations.
- Line Search methods.
- Unconstrained minimization algorithms.
- Constrained minimization algorithms. Penalty and barrier methods, SQP and SLP methods.
Work in the course: Homeworks every week. One midterm and
final. A computer project.
Lecture Notes (Transparencies):

murty@umich.edu
![]()