—
Gelman Chapter 11.6-11.9 examples
26 Sep 2020
Use for outputs
local gelman_output esttab,b(1) se wide mtitle("Coef.") scalars("rmse sigma") ///
coef(_cons "Intercept" rmse "sigma") nonum noobs nostar var(15)
local gelman_output2 esttab,b(2) se wide mtitle("Coef.") scalars("rmse sigma") ///
coef(_cons "Intercept" rmse "sigma") nonum noobs nostar var(15)Chapter 11.6-11.9
11.6 Residual standard deviation and explained variance
11.7 External validation: checking fitted model on new data
11.8 Cross-validation
Leave one out cross-validation
clear
qui set obs 20
gen x=_n
local a=.2
local b=.3
local sigma=1
set seed 2141
gen y=`a'+`b'*x + rnormal(0,`sigma')
gen outlier=" <-- outlier" if _n==17
twoway lfit y x || scatter y x ,mlabel(outlier) mlabc(blue)|| lfit y x if _n!=17 ///
,legend(off) ytitle(y) ylab(0(2.5)7.5) 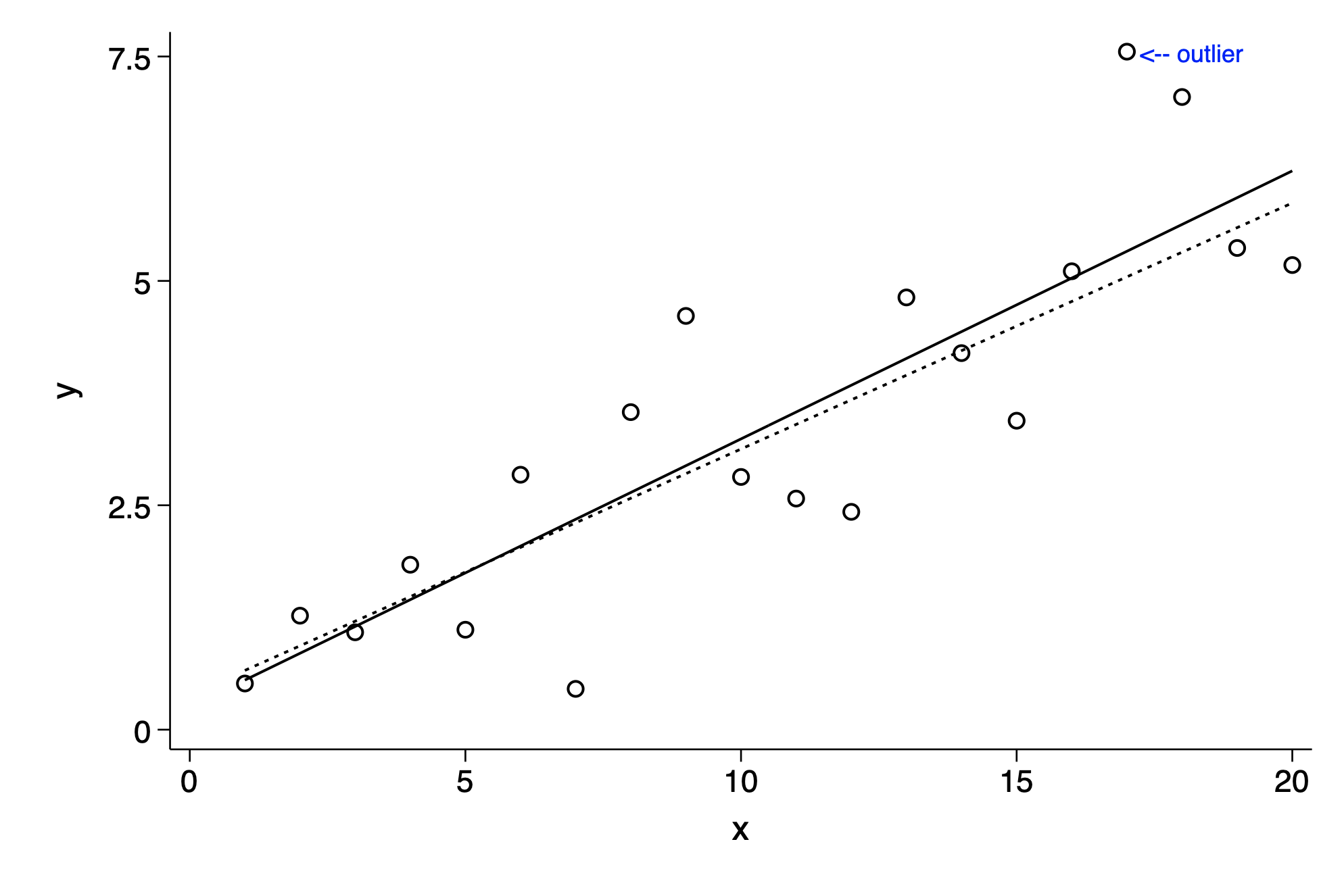
regress y x
predict yhat
predict yresid,resid
predict yhat_std,stdp
local yhat=yhat[17]
local yhat_std=yhat_std[17]
regress y x if _n!=17
predict yhat2
predict yresid2,resid
predict yhat2_std,stdp
local yhat2=yhat2[17]
local yhat2_std=yhat2_std[17]
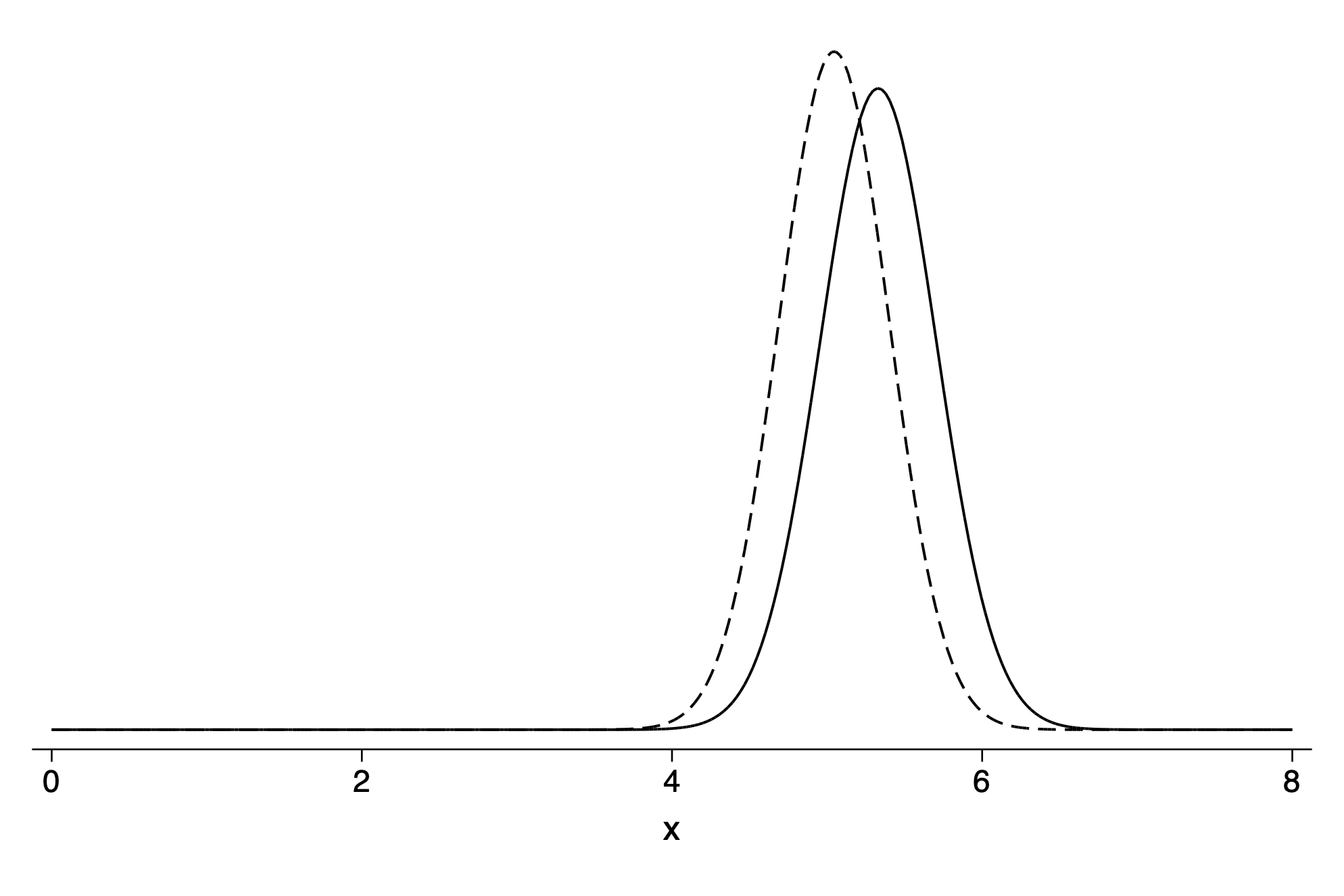
twoway (function y=normalden(x,`yhat',`yhat_std'), range(0 8)) ///
(function y=normalden(x,`yhat2',`yhat2_std'), range(0 8)) ,yscale(off) ///
legend(off)Prediction for outlier point from regression including outlier (solid line) and regression excluding outlier (dashed line)
There is a user developed program that does LOO cross-validation called cv_regress If it is not installed you can install it (only once) from the SSC archive.
ssc install cv_regressregress y x
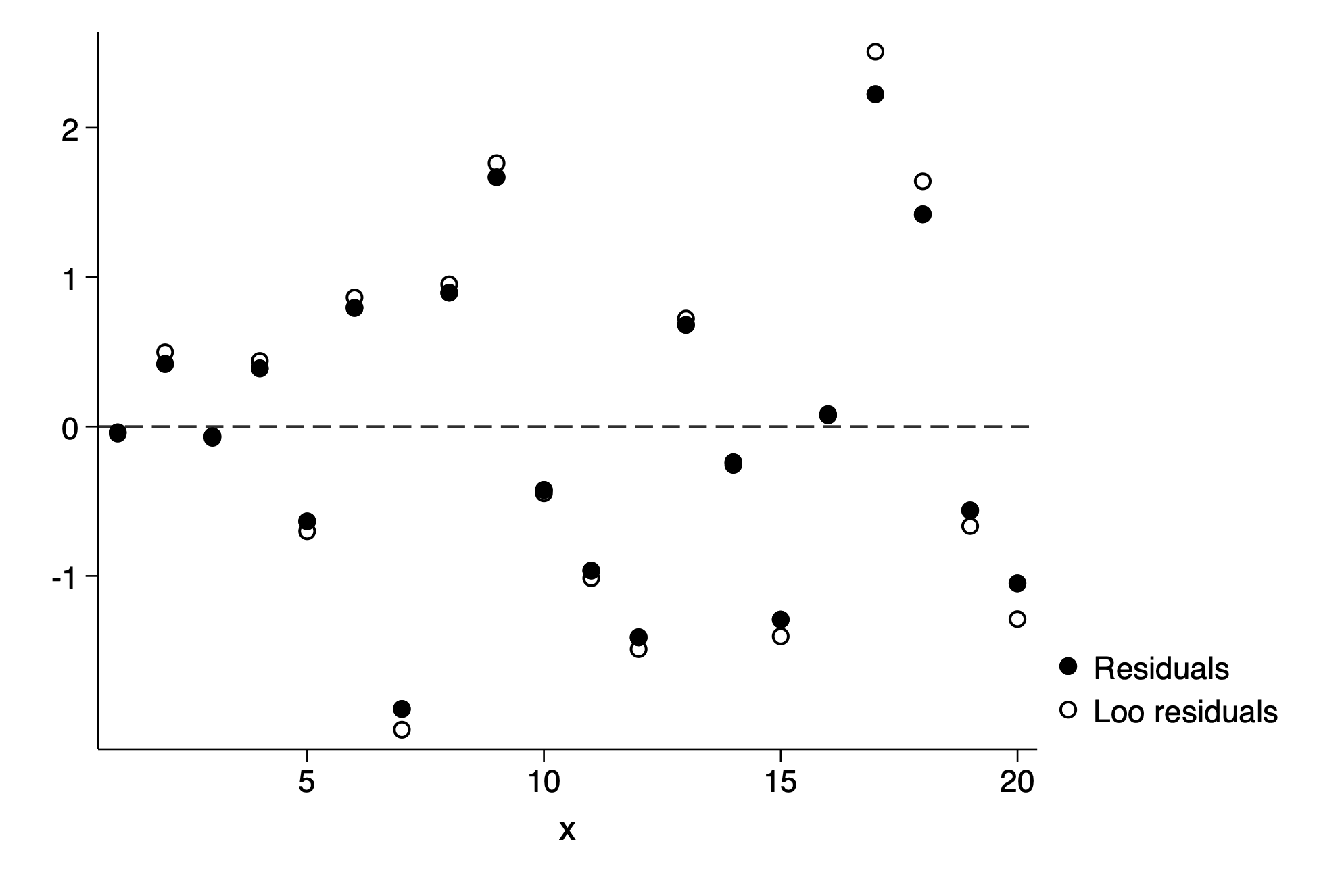
predict resid,resid
cv_regress, generr(resid_loo)
twoway scatter resid x || scatter resid_loo x , yline(0,lp(dash)) ///
ylab(-1(1)2) xlab(5(5)20) legend(label(2 "Loo residuals")) Source │ SS df MS Number of obs = 20
─────────────┼────────────────────────────────── F(1, 18) = 48.10
Model │ 59.2923422 1 59.2923422 Prob > F = 0.0000
Residual │ 22.1874673 18 1.23263707 R-squared = 0.7277
─────────────┼────────────────────────────────── Adj R-squared = 0.7126
Total │ 81.4798095 19 4.28841102 Root MSE = 1.1102
─────────────┬────────────────────────────────────────────────────────────────
y │ Coef. Std. Err. t P>|t| [95% Conf. Interval]
─────────────┼────────────────────────────────────────────────────────────────
x │ .2985991 .0430533 6.94 0.000 .2081474 .3890508
_cons │ .2540735 .5157423 0.49 0.628 -.8294608 1.337608
─────────────┴────────────────────────────────────────────────────────────────
Leave-One-Out Cross-Validation Results
─────────────────────────┬───────────────
Method │ Value
─────────────────────────┼───────────────
Root Mean Squared Errors │ 1.1601
Log Mean Squared Errors │ 0.2971
Mean Absolute Errors │ 0.9445
Pseudo-R2 │ 0.67117
─────────────────────────┴───────────────
A new Variable -resid_loo- was created with (y-E(y_-i|X))
Fast leave out one cross-validation
Summarizing prediction error using the log score and deviance
Overfitting and AIC
Demonstration of adding pure noise predictors to the model
Using the children’s test score data
local gelman_output3 esttab,b(1) se wide mtitle("Coef.") scalars("rmse sigma") ///
stats(r2,fmt(2)) coef(_cons "Intercept" rmse "sigma") nonum noobs nostar var(15)
import delimited https://raw.githubusercontent.com/avehtari/ROS-Examples/master/KidIQ/data/kidiq.csv, clear
qui regress kid_score i.mom_hs c.mom_iq
`gelman_output3'
cv_regress
* With noise predictors
set seed 29922
drawnorm noise1 noise2 noise3 noise4 noise5
qui regress kid_score i.mom_hs c.mom_iq noise1-noise5
`gelman_output3'─────────────────────────────────────────
Coef.
─────────────────────────────────────────
0.mom_hs 0.0 (.)
1.mom_hs 6.0 (2.2)
mom_iq 0.6 (0.1)
Intercept 25.7 (5.9)
─────────────────────────────────────────
r2 0.21
─────────────────────────────────────────
Standard errors in parentheses
Leave-One-Out Cross-Validation Results
─────────────────────────┬───────────────
Method │ Value
─────────────────────────┼───────────────
Root Mean Squared Errors │ 18.2024
Log Mean Squared Errors │ 5.8031
Mean Absolute Errors │ 14.4870
Pseudo-R2 │ 0.20299
─────────────────────────┴───────────────
Now a second regression adding only the noise predictors
─────────────────────────────────────────
Coef.
─────────────────────────────────────────
0.mom_hs 0.0 (.)
1.mom_hs 5.9 (2.2)
mom_iq 0.6 (0.1)
noise1 -0.7 (0.9)
noise2 0.6 (0.9)
noise3 0.7 (0.9)
noise4 0.6 (0.9)
noise5 0.9 (0.9)
Intercept 26.1 (5.9)
─────────────────────────────────────────
r2 0.22
─────────────────────────────────────────
Standard errors in parentheses
Recognizing overfitting
R2 appears to go up slightly, R2 .22 but the regression also gives an adjusted R2= .21
which adds a penalty for extra noise predictors that do nothing.
Or from the cross-validation you can also see that the root mean squared error has actually increased and consequently the R2 has decreased
. cv_regress
Leave-One-Out Cross-Validation Results
─────────────────────────┬───────────────
Method │ Value
─────────────────────────┼───────────────
Root Mean Squared Errors │ 18.3409
Log Mean Squared Errors │ 5.8183
Mean Absolute Errors │ 14.5802
Pseudo-R2 │ 0.19165
─────────────────────────┴───────────────