
| Algorithm for Isothermal Reactor Design | top |

Example: The elementary liquid phase reaction
![]()
is carried out isothermally in a CSTR. Pure A enters at a volumetric flow rate of 25 dm3/s and at a concentration of 0.2 mol/dm3.
What CSTR volume is necessary to achieve a 90% conversion when k = 10 dm3/(mol*s)?
|
Mole Balance |
|
|
Rate Law |
|
|
Stoichiometry |
liquid phase (v = vo) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Combine |
|
|
Evaluate |
at X = 0.9,
|
|
V = 1125 dm3 |
|
|
Space Time 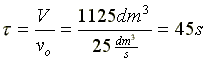 |
Here are some links to example problems. You could also use these problems as self tests.
The following movies were made by the students of Professor Alan Lane's chemical reaction engineering class at the University of Alabama Tuscaloosa
| Applications/Examples of the CRE Algorithm | top |
| Gas Phase Elementary Reaction | Additional Information | ||
|---|---|---|---|
 |
only A fed |
P0 = 8.2 atm |
 |
|
T0 = 500 K |
CA0 = 0.2 mol/dm3 |
||
|
k = 0.5 dm3/mol-s |
vo = 2.5 dm3/s |
||
Solve for X = 0.9
Applying the algorithm to the above reaction occurring in a Batch,
CSTR, and PFR.
| Batch | CSTR | PFR | |
|---|---|---|---|
| Mole Balance: |

|

|
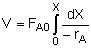
|
| Rate Law: |
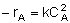
|
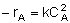
|
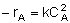
|
| Stoichiometry: |
Gas: V = V0 |
Gas: T =T0, P =P0 |
Gas: T = T0, P = P0 |
|
Per Mole of A:
|
Per Mole of A:
|
||

|

|

|
|
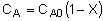
|
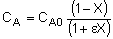
|
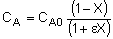
|
|
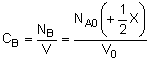
|

|

|
|

|

|

|
|
| Combine: |

|
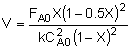
|
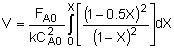
|
| Integrate |
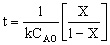
|

|
|
| Evaluate | 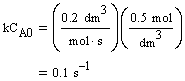 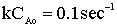 |
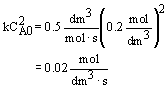  |
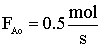 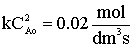 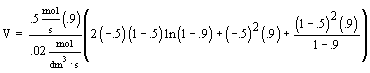 |
| For X = 0.9: | 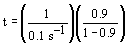 |
V = 680.6 dm3 |
V = 90.7 dm3 |
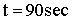 |
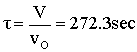 |
 |
| Reversible Reactions | top |
To determine the conversion or reactor volume for reversible reactions, one must first calculate the maximum conversion that can be achieved at the isothermal reaction temperature, which is the equilibrium conversion. (See Example 3-8 in the text for additional coverage of equilibrium conversion in isothermal reactor design.)
Equilibrium Conversion, Xe
From Appendix C:
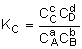
Example: Determine Xe for a PFR with no pressure drop, P = P0
Given that the system is gas phase and isothermal, determine the reactor volume when X = 0.8 Xe.
| Reaction | Additional Information | |
|---|---|---|
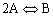
|
CA0 = 0.2 mol/dm3 |
k = 2 dm3/mol-min |
First calculate Xe:
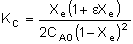
X = 0.8Xe = 0.711
 One could then use Polymath to determine the volume of the PFR. The corresponding
Polymath program is shown below.
One could then use Polymath to determine the volume of the PFR. The corresponding
Polymath program is shown below.
| ODE (Polymath) Solutions to CRE Problems | top |
Equations
Plot of X vs. V
Results in Tabular Form
A volume of 94 dm3 (rounding up from slightly more than 93 dm3) appears to be our answer.

| General Guidelines for California Problems | top |
Every state has an examination engineers must pass to become a registered professional engineer. In the past there have typically been six problems in a three hour segment of the California Professional Engineers Exam. Consequently one should be able to work each problem in 30 minutes or less. Many of these problems involve an intermediate calculation to determine the final answer.
Some Hints:
|
| PBR with Pressure Drop | top |
Note: Pressure drop does NOT affect liquid phase reactions
Sample Question:
Analyze the following second order gas phase reaction that occurs isothermally in a PBR:
![]()
Mole Balance
![]()
Must use the differential form of the mole balance to separate variables
Rate Law
Second order in A and irreversible:![]()
Stoichiometry
![]()
![]()
Need to find (P/P0) as a function of W (or V if you have a PFR).
Pressure Drop in Packed Bed Reactors
Ergun Equation |
 |
Variable Gas Density |
|
let |
|
where |
 |
let |
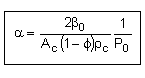 |
then |
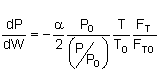 |
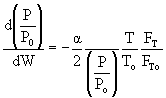 |
English-
Espanol-
Svenska-
We will use this form for multiple reactions: |
||
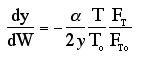  We will use this form for single reactions: |
||
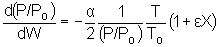 |
||
Isothermal Operation |
||
recall that |
||
notice that |
||
The two expressions are coupled ordinary differential equations. We can
solve them simultaneously using an ODE solver such as Polymath. For the special case of
isothermal operation and epsilon = 0, we can obtain an analytical solution. |
||
Analytical Solution![]() , [e], PFR with
, [e], PFR with![]()
 CAUTION: Never use this form if
|
||
Combine |
|
Solve |
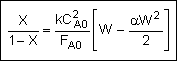 |
Could now solve for X given W, or for W given X.
For gas phase reactions, as the pressure drop increases, the concentration decreases,
resulting in a decreased rate of reaction, hence a lower conversion when compared to a
reactor without a pressure drop.
Here are some links to example problems dealing with packed bed reactors. You could
also use these problems as self tests.
POLYMATH
Consider the following gas phase reaction carried out isothermally in a packed bed
reactor. Pure A is fed at a rate of 2.5 moles/s and with![]()
![]() , and α =
0.0002 kg-1.
, and α =
0.0002 kg-1.
2A![]() B
B
Mole Balance
![]()
Rate Law
Elementary![]()
Stoichiometry
Gas with T = T0
A![]() B/2
B/2
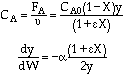
POLYMATH will combine everything - You do not need the combine step. Thank you POLYMATH

![]()
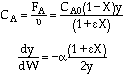
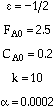
![]()
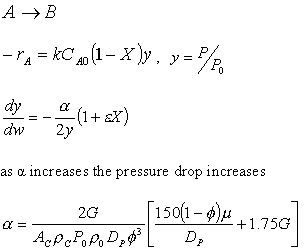
Laminar Flow, Fix P0, ρ0, 
ρ0 = P0(MW)/RT0
ρ0P0∼P02
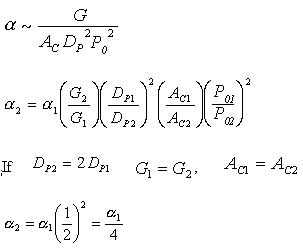

Increasing the particle diameter descreases the pressure drop and increases the rate and conversion.
However, there is a competing effect. The specific reaction rate decreases as the particle size increases, therefore so deos the conversion.
k ∼ 1/Dp
|
DP1 > DP2 |

The larger the particle, the more time it takes the reactant to get in and out of the catalyst particle. For a given catalyst weight, there is a greater external surgace area for smaller particles than larger particles. Therefore, there are more entry ways into the catalyst particle.
In CD-ROM chapter 12, we will learn that effectiveness factor decreases as the particle size increases
![]()
| Engineering Analysis - Critical Thinking and Creative Thinking | top |
We want to learn how the various parameters (particle diameter, porosity, etc.) affect the pressure drop and hence conversion. We need to know how to respond to "What if" questions, such as:
"If we double the particle size, decrease the porosity by a factor of 3, and double the pipe size, what will happen to D P and X?"
(See Critical Thinking in Preface page xx. e.g., Questions the probe consenquences)
To answer these questions we need to see how a varies with these parameters.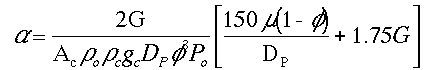
Turbulent Flow
Compare Case 1 and Case 2:
For example, Case 1 might be our current situation and Case 2 might be the parameters we want to change to.

For constant mass flow through the system![]() = constant
= constant
Laminar Flow
![]()
Here are more links to example problems dealing with packed bed reactors. Again, you could
also use these problems as self tests.
| Measures Other Than Conversion | top |
Uses:
A. Membrane reactors
B. Multiple reaction
Liquids: Use concentrations, I.E. CA
![]()
1. For the elementary liquid phase reaction ![]() carried out in a CSTR, where V, vo, CAo, k, and Kc are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry are:
carried out in a CSTR, where V, vo, CAo, k, and Kc are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry are:
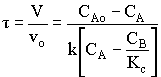
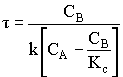
There are two equations, two unknowns, CA and CB
Gases: Use Molar Flow Rates, I.E. FI

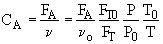

2. If the above reaction, ![]() ,carried out in the gas phase in a PFR, where V, vo,CAo,k, and Kc are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry yield, for isothermal operation (T=To) and no pressure drop (DP=0) are:
,carried out in the gas phase in a PFR, where V, vo,CAo,k, and Kc are given and the feed is pure A, the combined mole balance, rate laws, and stoichiometry yield, for isothermal operation (T=To) and no pressure drop (DP=0) are:

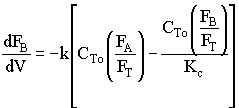
![]()
Use Polymath to plot FA and FB down the length of the reactor.
For isothermal microreactors, we use the same equations as a PFR as long as the flow is not laminar. If the flow is laminar, we must use the techniques discussed in chapter 13. See example 4.8 of the text.
| Membrane Reactors | top |
Membrane reactors can be used to achieve conversions greater than the original equilibrium value. These higher conversions are the result of Le Chatelier's Principle; you can remove one of the reaction products and drive the reaction to the right. To accomplish this, a membrane that is permeable to that reaction product, but is impermeable to all other species, is placed around the reacting mixture.
Example: The following reaction is to be carried out isothermally in a membrane reactor with no pressure drop. The membrane is permeable to Product C, but it is impermeable to all other species.
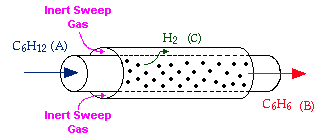 |
For membrane reactors, we cannot use conversion. We have to work in terms of the molar flow rates FA, FB, FC.
Polymath Program
Mole Balances |
|
Rate Laws |
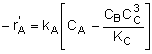 |
| |
|
| |
|
Combine |
Polymath will combine for you-- Thanks Polymath...you rock! |
Parameters |
|
Solve |
Polymath |
Here are links to example problems dealing with membrane reactors. You could also use these problems as self tests.
| Semibatch Reactors p. 190 | top |
Semibatch reactors can be very effective in maximizing selectivity in liquid phase
reactions.
![]() to Selectivity
to Selectivity
The reactant that starts in the reactor is always the limiting reactant.
| 1. Molar Basis | 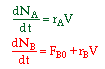 |
||
| 2. Concentration Basis | 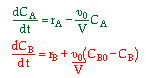 |
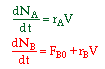 |
|
| 3. Conversion | |||
| For constant molar feed: | ||
| For constant density: | ||
Use the algorithm to solve the remainder of the problem.
Example: Elementary Irreversible Reaction
Consider the following irreversible elementary reaction:
-rA = kCACB
The combined mole balance, rate law, and stoichiometry may be written in terms of number of moles, conversion, and/or concentration:
| Conversion | Concentration | Number of Moles |
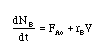 |
Polymath Equations:
| Conversion | Concentration | Moles |
d(X)/d(t) = -ra*V/Nao |
d(Ca)/d(t) = ra - (Ca*vo)/V |
d(Na)/d(t) = ra*V |
ra = -k*Ca*Cb |
d(Cb)/d(t) = rb + ((Cbo-Cb)*vo)/V |
d(Nb)/d(t) = rb*V + Fbo |
Ca = Nao*(1 - X)/V |
ra = -k*Ca*Cb |
ra = -k*Ca*Cb |
Cb = (Nbi + Fbo*t - Nao*X)/V |
rb = ra |
rb = ra |
V = Vo + vo*t |
V = Vo + vo*t |
V = Vo + vo*t |
Vo = 100 |
Vo = 100 |
Vo = 100 |
vo = 2 |
vo = 2 |
vo = 2 |
Nao = 100 |
Fbo = 5 |
Fbo = 5 |
Fbo = 5 |
Nao = 100 |
Ca = Na/V |
Nbi = 0 |
Cbo = Fbo/vo |
Cb = Nb/V |
k = 0.1 |
k = 0.01 |
k = 0.01 |
Na = Ca*V |
||
X = (Nao-Na)/Nao |
Polymath Screenshots:
| Conversion | Concentration |
Consider the following reversible reaction:
Everything is the same as for the irreversible case, except for the rate law:
At equilibrium, -rA=0, then
![]()

See Also:
![]() Web Module on Reactive Distillation
Web Module on Reactive Distillation
![]() You Rate Some Wetlands Critical Thinking Questions
You Rate Some Wetlands Critical Thinking Questions
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .