Research
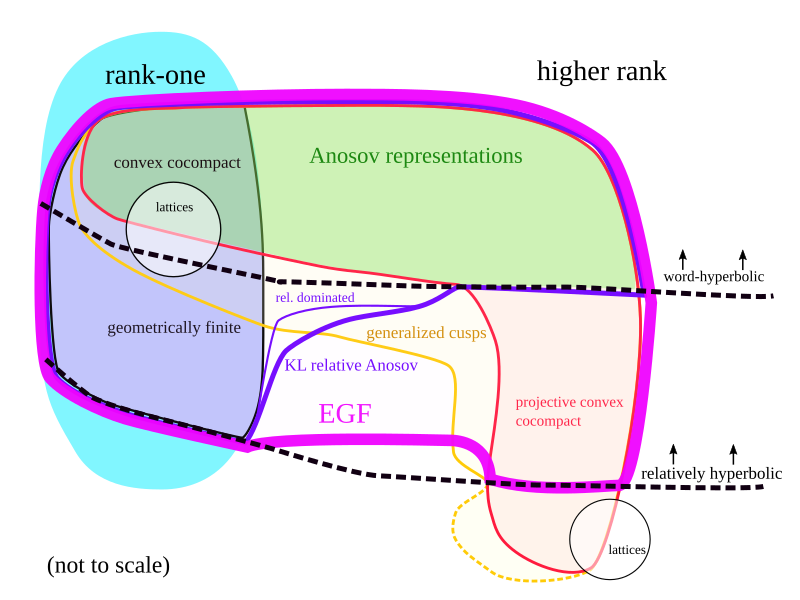
The main theme of my research is the interaction between geometric structures on manifolds, geometric group theory, and discrete subgroups of Lie groups. Mostly, this means that I work with actions of groups with rich coarse geometry (such as hyperbolic and relatively hyperbolic groups) on homogeneous spaces (like symmetric spaces, or projective space and other flag manifolds). Important examples include convex cocompact and geometrically finite subgroups of SL(2, R) and SL(2, C), as well as higher-rank analogs, such as Anosov subgroups and their generalizations.

Published and accepted articles
-
(with K. Mann and J.F. Manning) Topological stability of relatively hyperbolic groups acting on their boundaries. Math. Z. 312, 5, 2026.
-
(with M. Islam) Morse properties in convex projective geometry. Adv. Math., 479:110430, 2025.
-
(with S. Douba, B. Fléchelles, and F. Zhu) Cubulated hyperbolic groups admit Anosov representations, 2023. To appear in Geometry & Topology.
-
(with A. Traaseth) Combination theorems for geometrically finite convergence groups. To appear in Algebraic and Geometric Topology.
-
(with K. Mann and J.F. Manning) Stability of hyperbolic groups acting on their boundaries, 2022. To appear in Groups, Geometry, and Dynamics.
-
Dynamical properties of convex cocompact actions in projective space. J. Topol., 16(3):990-1047, 2023.
Preprints
-
Dehn filling in semisimple Lie groups. arXiv: 2502.17592, 2025. Submitted.
-
(with K. Tsouvalas) Singular value gap estimates for free products of semigroups. arXiv:2409.20330, 2024. Submitted.
-
(with A. Guilloux) Limits of limit sets in rank-one symmetric spaces. arXiv:2407.04301, 2024. Submitted.
-
Examples of extended geometrically finite representations. arXiv:2311.18653, 2023.
-
An extended definition of Anosov representation for relatively hyperbolic groups. arXiv:2205.07183, 2022. Submitted.
PhD thesis: Higher-rank generalizations of convex cocompact and geometrically finite dynamics.
Talk slides and videos
Anosov representations of cubulated hyperbolic groups
slides | video
Dehn filling in semisimple Lie groups
slides
Combination theorems for geometrically finite convergence groups (NCNGT, June 2023)
video (part 1) | video (part 2)
Topological stability for (relatively) hyperbolic boundary actions (GTiNY, June 2023)
slides
Extended geometrically finite representations (STDC, March 2022)
slides
Extended convergence dynamics and relative Anosov representations (December 2021)
slides
Expansion/contraction dynamics for non-strictly convex projective manifolds (GTA Philadelphia, June 2021)
slides
Group actions on boundaries of convex divisible domains (November 2019)
slides
Gallery
Coxeter automaton
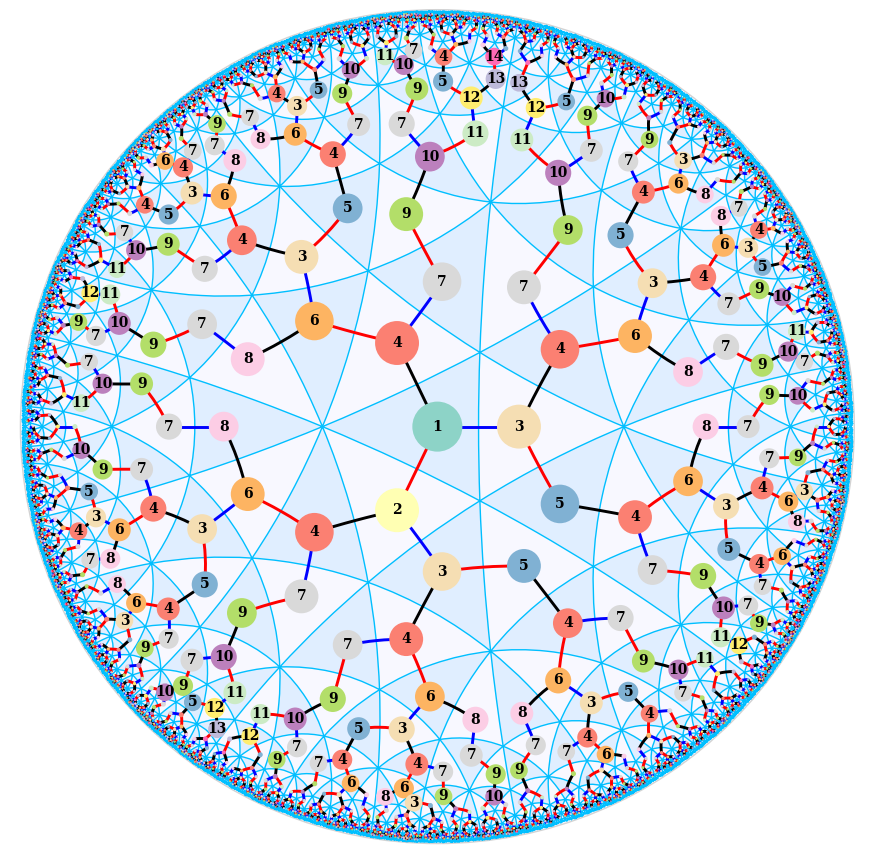
A shortlex automatic structure for a (3,3,4) triangle group in the hyperbolic plane, drawn using my geometry_tools Python package. Each numbered vertex is a state in a finite state automaton, generated using the kbmag program.
This image was originally created for the postcard session of the 2021 Nearly Carbon Neutral Geometric Topology conference.
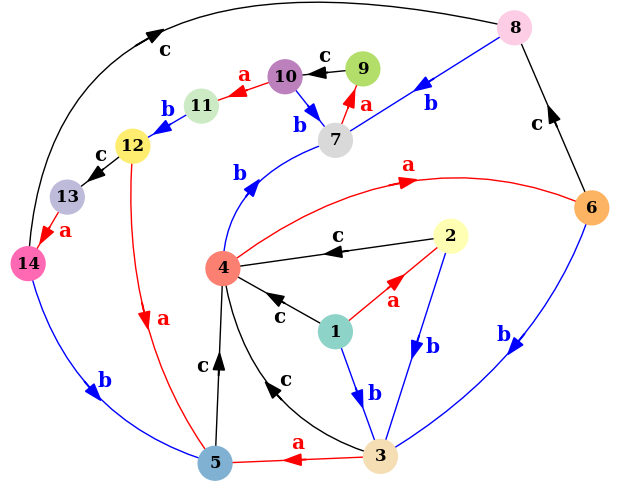
Figure-eight knot group automaton
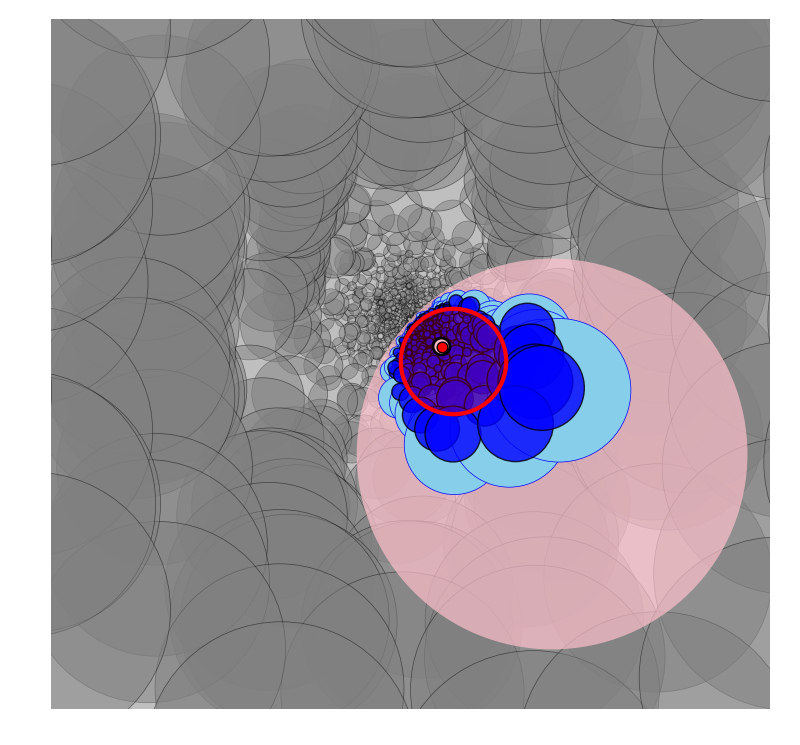
Pontryagin spheres

Animated version (41MB file) | Interactive version (5MB file, less detail)


